In dieser Sendung von Telekolleg-Physik werden Inhalte der vorhergehenden fortgeführt. Energie kann in anderer Form als nur als Lageenergie vorliegen. Auch in einer Bewegung steckt Energie. Die verschiedenen Energieformen lassen sich ineinander umwandeln, dabei bleibt die Gesamtenergie erhalten. Die Sendung gliedert sich in folgende Abschnitte:

Kinetische Energie

Mit Hubarbeit wird Lageenergie bereitgestellt

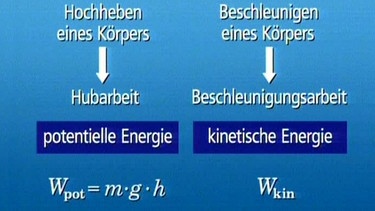
In der letzten Folge wurde der Begriff Hubarbeit eingeführt; damit wird Lageenergie bereitgestellt.

Die S-Bahn beschleunigt, da elektrische Energie zugeführt wird

Aber es gibt noch andere Möglichkeiten, mittels Arbeit eine erhöhte Energie zu erreichen. Beim Anfahren einer S-Bahn auf waagrechter Strecke wird elektrische Energie zugeführt, um die Geschwindigkeit zu erhöhen.

Zusammenhang von Arbeit und Energie

Man spricht deshalb von Beschleunigungsarbeit. Diese führt zu mehr Bewegungsenergie. Analog zur potenziellen Energie gibt es auch hier einen Fachbegriff, der diesmal aus der griechischen Sprache entnommen wurde: kinetische Energie (Kinetik = Lehre von der Bewegung).

Herleitung der Formel für die kinetische Energie

Für die kinetische Energie lässt sich mit dem Vorwissen aus früheren Sendungen eine Formel herleiten: Arbeit gleich Kraft mal Weg; dann für F und s jeweils andere Formeln einsetzen und man erhält: W_beschl = E_kin = 0,5·m·v². Damit kann für Anwendungen, bei denen die Geschwindigkeit und die Masse bekannt sind, die Bewegungsenergie berechnet werden.

Energiebedarf für die Beschleunigung von null auf 250 km/h

Gleichzeitig ist damit klar, wie viel Arbeit nötig ist, um den Gegenstand von null auf die Endgeschwindigkeit zu beschleunigen. Bei den Berechnungen mag immer wieder Unsicherheit bezüglich der Einheiten aufkommen.

Verwenden Sie diese Einheiten des SI-Systems

Wir profitieren vom internationalen Standardsystem (SI-System). Wenn für jede Größe, wie Masse bzw. Geschwindigkeit, die SI-Einheit verwendet wird, kg bzw. m/s, dann kommt das Ergebnis automatisch in seiner Standardeinheit heraus, hier die Einheit Joule für die Energie.

Umrechnungen: 3,6 km/h = 1 m/s; 1 kWh = 3,6 Mio Joule - klicken Sie bitte auf die Lupe.

In schwierigen Aufgaben werden aber nicht die Standardeinheiten benutzt, sondern z.B. km/h statt m/s oder kWh statt J. Dann sind Umrechnungen angesagt und es ist schön, wenn diese lästige Pflicht von einem Computer erledigt wird. Für die Bewegungsenergie eines ICE erhält man ein Ergebnis, das der elektrischen Energie für 200 Waschmaschinen-Ladungen entspricht.

Energieumwandlungen

Ein Skispringer wandelt Lageenergie in Bewegungsenergie

Ein Skispringer springt mit hoher Geschwindigkeit von der Sprungschanze ab, um eine möglichst weite Wurfparabel zu springen. Aber woher stammt diese kinetische Energie? Am Start hatte der Sportler eine hohe potenzielle Energie; diese wird bis zum Absprung deutlich vermindert. Deshalb vermuten wir, dass die Energie von der Form der Lageenergie in die Form der Bewegungsenergie umgewandelt wurde.

Verschiedene Hangneigungen, aber gleiche Höhe der beiden Wägelchen beim Start

Mit einem Experiment im Studio wird diese Vermutung überprüft. Zwei gleich schwere Wagen beschleunigen aus gleicher Höhe über zwei schiefe Ebenen mit deutlich unterschiedlicher Neigung. Am Auslauf wird jeweils die Endgeschwindigkeit gemessen.

Unterschiedliche Hangabtriebskräfte führen zu unterschiedlichen Beschleunigungen

Eine Momentaufnahme zeigt, dass die beschleunigende Kraft an der steileren Ebene größer ist.

Gleiche Endgeschwindigkeiten, deshalb gleiche kinetische Energien der Wägelchen

Aber offensichtlich wird dies durch die längere Beschleunigungsstrecke an der flacheren Ebene ausgeglichen, denn beide Wagen erreichen die gleiche Endgeschwindigkeit, wenn auch zu verschiedenen Zeitpunkten.

Mit der bekannten Masse von 0,5 kg wird daraus in beiden Fällen die kinetische Energie zu 2,94 J bestimmt.

Die potentielle Energie ist gleich der kinetischen Energie

Aufgrund der gleichen Starthöhe hatten beide Wagen zuvor auch die gleiche Lageenergie; diese Berechnung liefert den gleichen Energiewert von 2,94 J wie zuvor bei der kinetischen Energie. Mit diesem Ergebnis wird der Energieerhaltungssatz bestätigt.

Anwendungen zur Energieerhaltung

Energieerhaltungssatz der Mechanik

Die mechanische Energie bleibt immer dann erhalten, wenn Reibung ausgeschlossen werden kann und wenn keine äußere Kraft wirkt.

Energieerhaltung beim Oktoberfest

Bei einer Achterbahn ist die Energie am Start gleich null. Mit Hubarbeit wird zunächst Lageenergie bereit gestellt. In der Folge finden mehrere schnelle Umwandlungen zwischen Lage- und Bewegungsenergie statt.

Am Ende der Fahrt wird die Energie durch Reibungsarbeit wieder entzogen und die Startsituation wieder hergestellt.

Notbremsrampen am Zirler Berg in Österreich

Das Prinzip der Energieerhaltung ermöglicht auch die Berechnung von Wegstrecken. Am Zirler Berg in Österreich wird ein gefährliches Gefälle durch Notrampen abgesichert. Bei Bremsversagen lenkt der Autofahrer in eine seitliche schiefe Ebene, die Bewegungsenergie wird in Lageenergie umgewandelt und ein Kiesbett verhindert durch starke Reibung ein Zurückrollen von der höchsten Stelle.

Umwandlung von kinetischer Energie in Lageenergie

Welche Höhendifferenz der Notbremsrampe ist für eine Geschwindigkeit von 60 km/h nötig? Für Aufgaben dieser Art muss die Masse gar nicht bekannt sein, denn sie kommt in beiden Energieformeln vor. Es wird eine Höhe von fast 15 m errechnet!

Beim Bremsen geht mechanische Energie in Wärme über.

Bei funktionierenden Bremsen "verschwindet" Lageenergie, ohne dass sich die Bewegungsenergie erhöht. Diese Abweichung von der Energieerhaltung der Mechanik hängt offensichtlich mit der enormen Temperaturerhöhung an den Bremsscheiben zusammen.

Rotationsenergie

Altes Blechauto mit Schwungradantrieb

In manchen alten Spielzeugautos wird Energie in der Rotation einer Schwungscheibe gespeichert und dann in Bewegung umgewandelt. Moderne Entwicklungen bei Stadtbussen verwenden ebenfalls Schwungsysteme, um beim Anhalten einen Teil der Bewegungsenergie in Form von Rotationsenergie zu speichern und sie beim Anfahren wieder freizusetzen.

Spielzeugauto auf einer Schiefen Ebene mit Looping

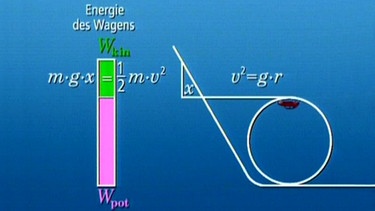
Die Notwendigkeit von Rotationsenergie wird auch bei einem Looping sichtbar. Bei zu geringer Starthöhe fällt der Wagen vor dem höchsten Punkt aus der Bahn.

Zusatzhöhe x für die Mindestgeschwindigkeit beim Looping

Die nötige Zusatzhöhe lässt sich mit einem Energieansatz berechnen. Sie beträgt die Hälfte des Radius des Loopings.

Eine weitere mechanische Energieform?

Bestimmung der Abschussgeschwindigkeit des Balls mit zwei Lichtschranken und Computer

Die Energieerhaltung ermöglicht Vorhersagen zum Ablauf eines Experiments. Bei einem Geschicklichkeits-Spielzeug schleudert eine entspannte Feder einen Plastikball in die Höhe, der dann mit einem kleinen Korb wieder aufgefangen werden muss. Die Startgeschwindigkeit kann mit zwei übereinander postierten Lichtschranken bestimmt werden.

Bestimmung der Schusshöhe bei gegebener Startgeschwindigkeit

Damit lässt sich über die Gleichsetzung von kinetischer und potenzieller Energie die maximale Höhe bestimmen.

Eine gespannte Feder speichert Energie.

Aber woher kommt die kinetische Energie beim Start? Offensichtlich ist der Federmechanismus in der Lage, Energie bereit zu stellen. Dies wird das Thema der nächsten Folge sein.