In dieser Sendung von Telekolleg-Physik werden die Begriffe Arbeit, Energie und Leistung auf Drehbewegungen angewendet. Eine zentrale Rolle spielt dabei der Begriff Drehmoment, bei dem der Kraftaufwand mit dem Hebelarm verrechnet wird. Die Sendung gliedert sich in folgende Abschnitte:

Drehmoment

Bei einem Reifenwechsel kommt es darauf an, dass man geeignetes Werkzeug hat. Oft ist beim serienmäßigen Bordwerkzeug der "Hebelarm" so kurz, dass eine zu stark angezogene oder angerostete Schraube nicht gelöst werden kann.

Radwechsel mit Pressluftwerkzeug (mit Drehmomentbegrenzung)

In Werkstätten werden bequeme Pressluftschrauber verwendet, die zudem den Vorteil bieten, dass sie die Schrauben genau mit dem von der Autofirma vorgeschriebenen Drehmoment anziehen.

Kraft 50 N, Hebelarm 0,40 m -> Drehmoment 20 Nm

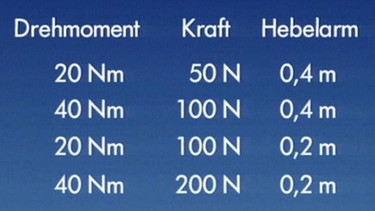
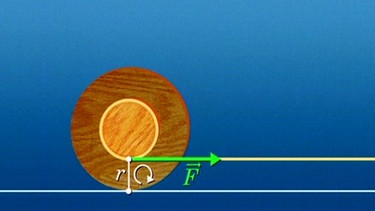
Im Studio ist ein Pkw aufgestellt und für Messungen steht ein einfacher "Drehmomentschlüssel" zur Verfügung: Bei einem Radius von 0,40 m und einer Kraft von 50 N ergibt sich ein Drehmoment von 20 Newtonmeter (= 20 N·m = 20 Nm).

Kraft 100 N, Hebelarm 0,20 m -> Drehmoment 20 Nm

Genau das gleiche Drehmoment M von 20 Newtonmeter erhält man auch bei einem halbierten Radius von 0,20 m und der dann notwendigen doppelten Kraft von 100 N.

Tabelle von Messwerten mit unterschiedlichen Kräften und Hebelarmen

Bei verschiedenen Hebelarmen und den dabei gemessenen Kräften ist immer das Drehmoment gleich dem Produkt aus Kraft und Hebelarm.

Definition und Einheit des Drehmoments

Diese Definition beinhaltet auch die Festlegung für die Einheit des Drehmoments: [M] = 1 Nm. Diese Einheit ist bereits für die Arbeit bekannt, aber beim Drehmoment darf die Einheit Joule nicht verwendet werden.

Es zählt nur die Kraftkomponente senkrecht zum Hebelarm.

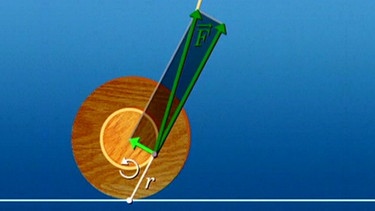
M darf auf keinen Fall mit einer Arbeit verwechselt werden; der Hebelarm ist immer senkrecht zur Kraft gerichtet und er beschreibt deshalb nie den Weg einer Kraftwirkung. Wenn die Kraft nicht senkrecht zum Hebelarm wirkt, dann zählt für das Drehmoment nur die Kraftkomponente senkrecht zum Hebelarm.

Beschleunigte Drehbewegung

Drehmoment und Winkelgeschwindigkeit bei einem Wasserrad

Im Alltag lassen sich viele Beispiele für Drehbewegungen finden, z.B. ein idyllisches Wasserrad an einer ehemaligen Mühle.

Modellversuch zum Wasserrad im Studio

Im Studio ist dazu ein Modellaufbau vorbereitet. Je größer die Kraft des Wasserstrahls, desto schneller setzt sich das Wasserrad in Bewegung.

Messversuch zum Zusammenhang von Drehmoment und Winkelgeschwindigkeit

Mit einem speziellen Messaufbau wird der Zusammenhang von Drehmoment und Winkelgeschwindigkeit untersucht: Ein Drehteller beginnt aufgrund einer Kraftwirkung zu rotieren und beschleunigt mit der Zeit immer mehr.

Detailaufnahme: Speichenrad mit Lichtschranke

Ein konstantes Drehmoment wird dadurch realisiert, dass am unteren Haltezylinder des Tellers eine Schnur aufgewickelt ist, an der ein Gewicht zieht. Die Schnur verläuft über eine Umlenkrolle. Diese ist ein Speichenrad und deshalb liegt es nahe, die Bewegung des Rades mit einer Lichtschranke zu registrieren.

Die Wertetabelle zeigt, dass die Winkelgeschwindigkeit proportional mit der Zeit anwächst.

Messergebnisse zum Zusammenhang von Drehmoment und Winkelgeschwindigkeit

Bei verdoppeltem Gewicht verdoppelt sich auch das Drehmoment. Dann wird eine bestimmte Winkelgeschwindigkeit in der halben Zeit erreicht. Analog zur linearen Bewegung nennt man den konstanten Quotienten Winkelbeschleunigung α.

In welche Richtung wird sich die Kabelrolle bewegen?

Die Drehrichtung ist jeweils durch die Richtung des Drehmoments festgelegt. Bei manchen Anwendungsbeispielen kann dies im Einzelfall durchaus ein überraschendes Ergebnis liefern.

Zugrichtung für eine Drehung nach rechts

Wenn man am losen Ende eines Kabels zieht, das auf einer Rolle aufgewickelt ist, dann bewegt sich die Rolle meistens zur Person hin.

Zugrichtung für eine Drehung nach links

Bei einer anderen Zugrichtung kann sich die Kabelrolle aber auch wegbewegen.

Rotationsenergie

Beim Jojo wandelt sich potenzielle Energie in Rotationsenergie und umgekehrt

Ein Jojo ist ein Spielzeug, das fast jeder kennt. Damit lassen sich Energieumwandlungen beobachten, bei denen die Rotationsenergie eine große Rolle spielt.

Oberer Umkehrpunkt des Riesenjojo: Die Rotationsenergie ist null.

Im oberen Umkehrpunkt liegt nur potentielle Energie vor. Diese wandelt sich fast vollständig in Rotationsenergie um. Die kinetische Energie der sehr langsamen Bewegung nach unten kann bei dem speziell konstruierten Riesen-Jojo vernachlässigt werden.

Herleitung der Rotationsenergie eines Rades

Für die Rotationsenergie eines Rades, bei dem nur der Ring eine gleichmäßig verteilte Masse m aufweist und die Speichen nicht zählen, wird eine Formel hergeleitet. Diese ist von der Formel für die kinetische Energie einer geradlinigen Bewegung abgeleitet und sieht deshalb sehr ähnlich aus.

Trägheitsmoment

Trägheitsmomente verschiedener rotationssymmetrischer Körper

Das Rad ist nur eine Möglichkeit, wie ein rotierender Gegenstand aufgebaut sein kann. Sind die Massen anders angeordnet, dann ergibt sich auch für die Formel der Rotationsenergie ein geringfügig anderer Term. Das Produkt m·r², zusammen mit einem Zahlenfaktor, der sich je nach Gegenstand ändert, wird als Trägheitsmoment J abgekürzt. Die Namenswahl soll an die Analogie zur trägen Masse m bei linearen Bewegungen erinnern.

Ein Hohl- und ein Vollzylinder gleicher Masse rollen eine schiefe Ebene abwärts.

In einem einfachen, aber sehr eindrucksvollen Experiment wird die Bedeutung des Trägheitsmoments ersichtlich. Zwei Zylinder haben genau die gleiche Masse. Sind sie gleich schnell, wenn sie gleichzeitig auf einer schiefen Ebene gestartet werden? Nein, denn der Hohlzylinder hat seine Masse weit mehr nach außen verlagert und deshalb ein größeres Trägheitsmoment. Deshalb beschleunigt der Hohlzylinder langsamer. In der Mechanik gibt es zu dieser Argumentation über Kräfte und Beschleunigungen stets eine davon unabhängige Alternative: Energiebetrachtungen. Der Hohlzylinder speichert bei gleicher Drehgeschwindigkeit mehr Rotationsenergie als der Vollzylinder. Bei gleicher Abnahme der potenziellen Energie bleibt für die lineare kinetische Energie bei der Bewegung nach unten ein geringerer Anteil als beim Vollzylinder; der Hohlzylinder ist deshalb langsamer.

Leistung und Drehmoment

Zusammenhang von Leistung, Drehmoment und Winkelgeschwindigkeit bei der Rotation

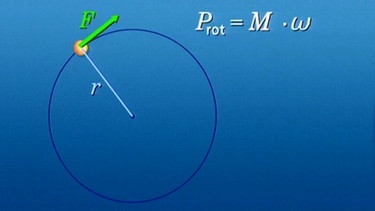
Die vielen Analogien zwischen einer linearen Bewegung und einer Kreisbewegung stärken das Vertrauen, dass dies auch für weitere Formeln gilt. Für die Leistung wurde in der letzten Sendung die Formel P = F·v hergeleitet. Übersetzt auf eine Kreisbewegung folgt: P = M·ω .

Welche maximale Winkelgeschwindigkeit hat das Jojo ganz unten?

Zum Abschluss der Sendung werden verschiedene Formeln der Sendung genutzt, um eine kompliziertere Rechenaufgabe zu lösen: Welche Rotationsgeschwindigkeit hat das große Jojo im unteren Umkehrpunkt? Wieder einmal bietet das Konzept der Energieerhaltung einen Zugang, um das Problem zu lösen.