Diese Sonden haben unser äußeres Planetensystem erforscht.

Satelliten erfahren an jedem Punkt des Raums eine Kraft, die vom Abstand zum Erdmittelpunkt abhängt. Beim Transport eines Satelliten in den Weltraum ist mechanische Arbeit nötig, dabei verändert sich seine kinetische und potenzielle Energie. Die Sendung gliedert sich in folgende Abschnitte:

Gravitationskraft

Die Sendung beginnt mit Szenen der Voyager-Missionen und verknüpft so diese letzte Sendung des Telekollegkurses Mechanik mit der ersten Sendung. Die 1977 gestarteten Sonden haben inzwischen längst unser Sonnensystem verlassen.

Vorher übermittelten sie beeindruckende Bilder von vier der insgesamt neun Planeten unseres Sonnensystems: von Jupiter, dem größten Planeten des Sonnensystems, von Saturn, dessen eindrucksvolles Ringsystem schon mit einfachen Ferngläsern zu erkennen ist, von Uranus, der nach neuesten Erkenntnissen ebenfalls über ein Ringsystem verfügt und von Neptun, dem äußersten der großen Planeten.

Um eine Weltraumreise über mehr als 10 Jahre erfolgreich gestalten zu können, müssen Wissenschaftler die Kräfte und die Bewegungen sehr genau vorhersagen können. Als Hilfsmittel verwenden sie den Begriff Gravitationsfeld, der sich auf einfache Weise aus dem Gravitationsgesetz ableiten lässt.

Der Halley-Komet; sein Schweif zeigt stets von der Sonne weg.

Zur Veranschaulichung einer Gravitationskraft wird angenommen, dass eine Raumsonde einen besonders kleinen Himmelskörper, z.B. einen Kometen erforschen soll.

Anziehungskraft zwischen einer Sonde und einem kleinen Kometen

Für die Anziehung zwischen den relativ kleinen Massen erhält man ein Ergebnis, bei dem nun noch der Abstand variiert werden kann.

Abhängigkeit der Gravitationskraft vom Abstand

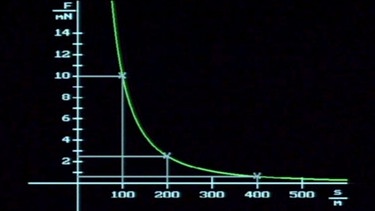
Die grafische Darstellung liefert eine stark abfallende Hyperbel: Direkt auf der Oberfläche des Kometen (r = 100 m) beträgt die Anziehung 1/100 N, bei doppeltem Abstand nur noch 1/400 N.

Die Anziehung nimmt daher bei größerem Abstand schnell ab.

Wie ausführliche Experimente bestätigen, nimmt die Gravitationskraft mit 1/r² ab. Sie ist aber dennoch auch in riesigen Entfernungen noch wirksam.

So kann die Gravitationskraft der Sonne den Riesenplaneten Neptun – 17 mal so schwer wie die Erde – in einer Entfernung von 4,5 Milliarden Kilometer auf seiner elliptischen Bahn halten!

Ein Ballon wird von einer mit Hochspannung geladenen Konduktorkugel angezogen.

Eine experimentelle Überprüfung ist bei den verschwindend kleinen Gravitationskräften zwischen Massen im Kilogrammbereich nicht möglich. Deshalb wird als Modellexperiment mit einem Bandgenerator experimentiert und die elektrische Anziehung zwischen Ladungen verschiedenen Vorzeichens betrachtet.

Vergleich der Messwerte mit der theoretischen Kurve

Diese elektrische Kraft weist das gleiche Abstandsverhalten auf wie die Gravitation.

Modellexperiment zum radialsymmetrischen Feld

Bei einer Kraft muss zusätzlich zur Stärke auch ihre Richtung untersucht werden. Gravitationskräfte sind stets vom Schwerpunkt der einen Masse zum Schwerpunkt der anderen Masse gerichtet. Eine kleine Probemasse wird stets zum Mittelpunkt einer großen Masse hingezogen. Man sagt: Die Gravitationskraft ist eine Zentralkraft.

Gravitationsfeld

Feldstärke = Kraft durch Masse des Probekörpers

Das Modellexperiment mit dem Bandgenerator sieht besonders eindrucksvoll aus, wenn gleichzeitig viele Probemassen angezogen werden. Die Kraftrichtungen verlaufen strahlenförmig zum zentralen Mittelpunkt. Um das Zentralobjekt herum ist für jeden Punkt des Raums festgelegt, wie groß die Anziehungskraft auf einen Probekörper ist. Dieser Befund regt an, eine Feldstärke zu definieren, indem man die Kraft durch die beliebige Masse des Probekörpers dividiert.

Radialsymmetrisches Gravitationsfeld

Als Feldlinien soll man sich die Bewegungslinien von zunächst ruhenden Probekörpern im Gravitationsfeld vorstellen.

Bei kleinen Distanzen erscheinen die Feldlinien parallel.

Hängt man zwei Lotgewichte im Studio nebeneinander auf, dann scheinen die Fäden parallel zu sein. Dies liegt daran, dass der Erdmittelpunkt, zu dem die Lotgewichte zeigen, so weit von der Erdoberfläche entfernt ist.

Arbeit im Gravitationsfeld

Die Formel "Kraft mal Weg" wäre hier falsch.

Nun wird ein Probekörper der Masse m₂ im Gravitationsfeld einer großen Masse m₁ bewegt. Wie groß ist die dafür notwendige Arbeit? Zunächst ist klar, dass es nur auf die Abstände zum Erdmittelpunkt am Anfang und am Ende ankommt, denn die zu überwindende Kraft wirkt radial und nicht tangential. Der Gegenstand darf bei konstantem Abstand beliebig seitlich verschoben werden, ohne dass dafür gearbeitet werden muss. Die Formel für die Arbeit lässt sich dann aber nicht einfach als "Kraft mal Weg" ansetzen, weil die Kraft nicht konstant ist. Die Herleitung der Formel finden Sie in Ihrem Begleitbuch.

Mit dieser Arbeit wird ein Satellit in eine geostationäre Umlaufbahn gebracht.

Zur Anwendung wird die Arbeit berechnet, mit der ein Satellit von der Erdoberfläche auf eine geostationäre Bahn gebracht wird. Das ist aber nur ein sehr kleiner Teil der tatsächlichen Arbeit für die Positionierung eines Satelliten.

Bei einem Raketenstart beansprucht alleine der Treibstoff 88% der Masse. Auch die restlichen 12% gehören nur zu einem sehr geringen Anteil zur Nutzlast.

Die Nutzmasse beträgt nur 0,5% der Startmasse.

Zum Beispiel transportierte die europäischen Rakete Ariane IV drei Satelliten der Gesamtmasse 2 t in eine geostationäre Bahn. Das Startgewicht von Rakete und Treibstoff betrug dabei 400 t.

Energie im Gravitationsfeld

Übersicht über die Formeln für Arbeit im Gravitationsfeld

Der Begriff Arbeit ist in der Mechanik immer eng mit potenzieller Energie verknüpft. Ein Satellit, an dem Arbeit verrichtet wurde, hat anschließend einen größeren Abstand zum Erdmittelpunkt und damit eine größere potenzielle Energie.

Umwandlung von kinetische Energie in Lageenergie in "unendlicher" Entfernung

Welche Arbeit bzw. potenzielle Energie ist nötig, damit ein Satellit das Gravitationsfeld verlassen kann? Um das zu berechnen, muss man in der Formel den Endabstand auf unendlich setzen. Dann verschwindet dieser Subtrahend, weil eins durch unendlich gleich null ist. Wie kann man diese Flucht aus dem Gravitationsfeld praktisch bewerkstelligen? Am besten dadurch, dass man dem Satelliten eine so hohe Startgeschwindigkeit mitgibt, dass die kinetische Energie der potenziellen Energie im "Unendlichen" entspricht.

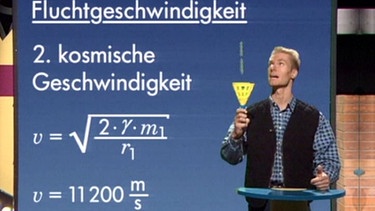
Mit einer Energiegleichung kann die erforderliche Geschwindigkeit berechnet werden.

Mit dieser Geschwindigkeit verlässt ein Satellit das Gravitationsfeld der Erde.

Sie ist unabhängig von der Masse m₁ des Satelliten und hängt nur von der Masse m₂ des Planeten ab, dessen Gravitationsfeld verlassen werden soll. Für die Erde beträgt diese Geschwindigkeit 11,2 km/s. Man nennt diese auch die 2. kosmische Geschwindigkeit.

Computersimulation: Die Startgeschwindigkeit ist zu klein.

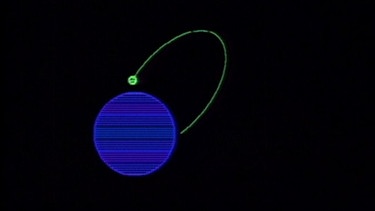
Die 1. kosmische Geschwindigkeit von 7,9 km/s ist nötig, um eine erdnahe Umlaufbahn zu erreichen. In einer Computersimulation werden Satelliten mit Geschwindigkeiten nahe der Fluchtgeschwindigkeit gestartet. Ist die Geschwindigkeit zu klein, dann kehrt der Satellit um und stürzt auf die Erde zurück.

Die Voyager-Sonden haben inzwischen nicht nur das Gravitationsfeld der Erde verlassen, sondern zusätzlich auch das viel stärkere Feld der Sonne.

Mit dieser Geschwindigkeit verlässt eine Raumsonde das Gravitationsfeld der Sonne.

Wenn man im Energieansatz die Sonnendaten, Masse und Abstand, einsetzt erhält man die 3. kosmische Geschwindigkeit von 42,1 km/s, die zur Flucht aus dem Sonnensystem ausreicht.