GRIPS Mathe 3 Wie werden Brüche dargestellt?
Brüche und Bruchzahlen richtig darstellen: So geht's.
Brüche lassen sich auf ganz unterschiedliche Art und Weise darstellen. Du kannst sie als Bruchzahl schreiben, sie in einer Grafik veranschaulichen oder sie in einem Zahlenstrahl einzeichnen.
Aufbau eines Bruchs
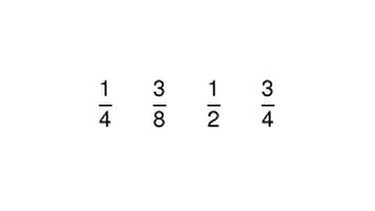
Ein Bruch ist immer so aufgebaut, dass über und unter dem Bruchstrich je eine Zahl steht. Dabei haben die beiden Zahlen unterschiedliche Bedeutungen:
Die Zahl unter dem Bruchstrich heißt Nenner. Sie "nennt" dir die Anzahl an gleich großen Teilen, in die du das Ganze zerlegen sollst.
Die Zahl über den Bruchstrich heißt Zähler. Der Zähler gibt an, wie viele von den gleich großen Teilen du nehmen sollst.
So stellst du fünf Sechstel her
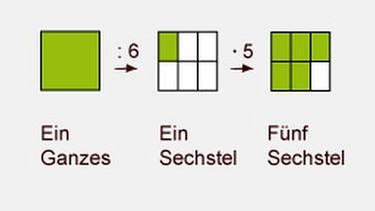
Der Bruch 5/6 bedeutet also: Ich teile ein Ganzes in sechs gleich große Teile und nehme fünf davon.
Merke: der Bruchstrich bedeutet "geteilt"!
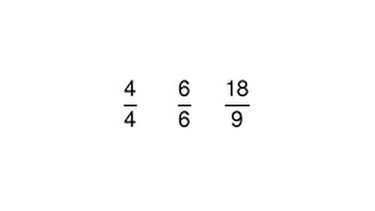
Verschiedene Arten von Brüchen
Es gibt verschiedene Arten von Brüchen. Hier lernst du sie kennen ...
Brucharten
Echte Brüche
Bei echten Brüchen ist der Zähler kleiner als der Nenner.
Brüche am Zahlenstrahl
Zum kompletten Zahlenstrahl - hier klicken!
Jeder Bruch lässt sich in einen Zahlenstrahl übertragen. Die nebenstehende Grafik zeigt dir eine Auswahl von Brüchen. Die Brüche wurden ihrer Größe nach zwischen zwei natürlichen Zahlen eingeordnet.