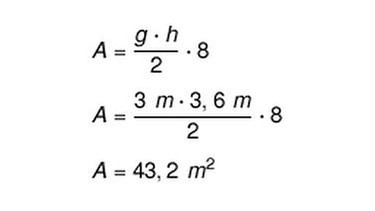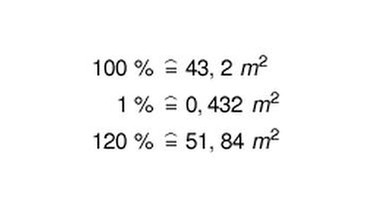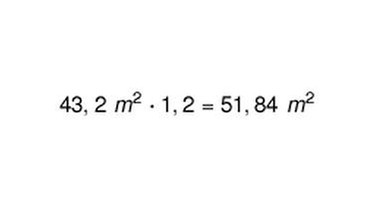Mach mit! Übung 2
Familie Sommer bekommt ein Partyzelt, dessen Grundfläche ein regelmäßiges Achteck mit einem Umfang von 24 m ist.
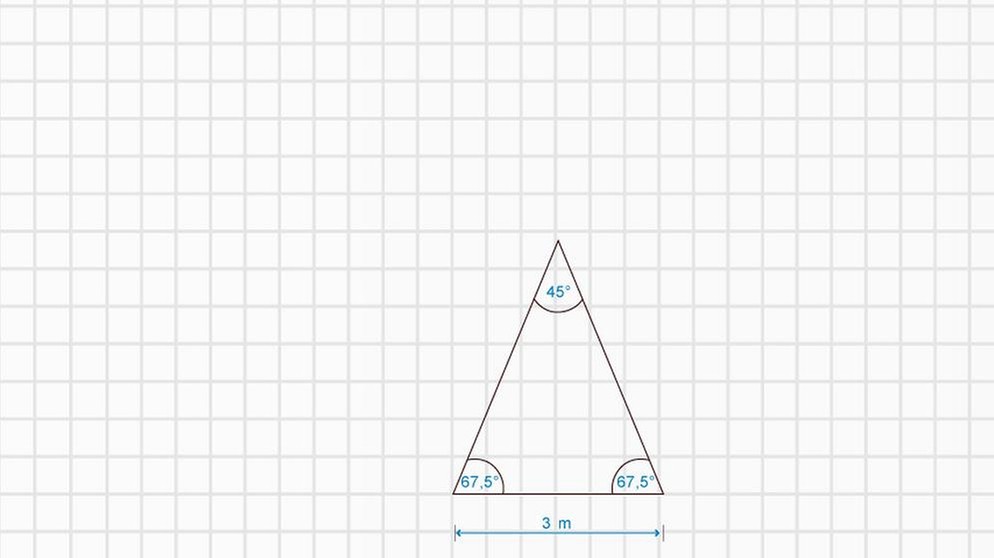
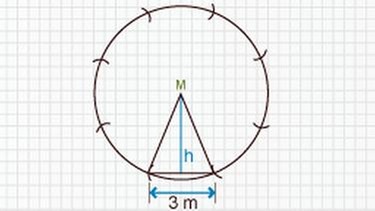
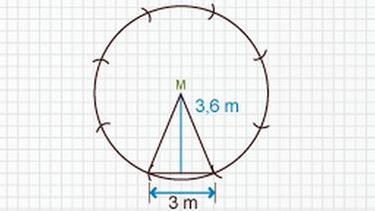
a. Zeichne die Grundfläche in geeignetem Maßstab auf ein kariertes Blatt Papier.
Hier siehst du die Lösung:
Schritt 1: Dreiecksseite und Winkel berechnen Der Umfang des Achtecks beträgt 24 m. Eine Seite ist also 24 m : 8 = 3 m lang. Als Maßstab wählst du am besten 1 : 100. Drei Meter in Wirklichkeit entsprechen 3 cm in der Zeichnung. Der Mittelpunktswinkel in einem regelmäßigen Achteck beträgt 360° : 8 = 45°. Die beiden anderen Winkel sind somit 67,5°. Zeichne eine Seite mit 3 cm mit den beiden Basiswinkeln ein.
b. Das Partyzelt soll einen Holzboden bekommen. Berechne seinen Flächeninhalt und rechne 20 % Verschnitt dazu. Entnimm die zur Berechnung notwendigen Maße deiner Zeichnung.
Lösung
Hilfe
Um die Fläche des Achtecks zu ermitteln, musst du erst den Flächeninhalt des Bestimmungsdreieckes berechnen und diesen Flächeninhalt mit 8 multiplizieren.
Die Höhe des Dreiecks misst du in der Skizze ab. Beachte dabei den Maßstab.
