Aufgabe
Die Ecken eines Quadrates liegen auf einer Kreislinie (siehe Skizze).
Der Flächeninhalt des Kreises beträgt 78,5 cm².
Berechne den Flächeninhalt der eingefärbten Fläche.
Hilfe
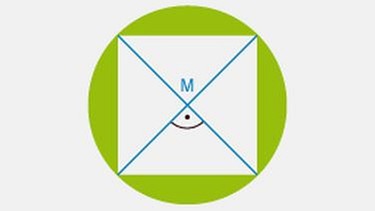
Um den Flächeninhalt der gefärbten Fläche zu bekommen, subtrahierst du den Flächeninhalt des Quadrats vom Flächeninhalt des Kreises.
Das Quadrat besteht aus vier rechtwinkligen Dreiecken. Daher kannst du die Seitenlänge des Quadrats mit dem Satz des Pythagoras bestimmen.
Die Katheten der rechtwinkligen Dreiecke sind dabei genauso groß wie der Radius des Kreises.
Radius Kreis
Allgemeine Formel (Flächeninhalt Kreis):
A (Kreis) = r² · π
Einsetzen in die Formel:
78, 5 = r² · 3,14 | : 3,14
25 = r² | √
5 cm = r
Antwort: Der Radius des Kreises beträgt 5 cm.
Seitenlänge Quadrat
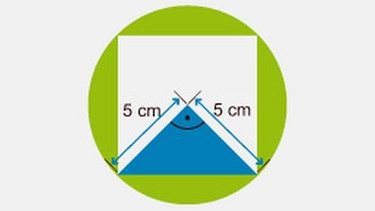
Mit dem Radius und dem Satz des Pythagoras kannst du jetzt die Seitenlänge des Quadrats berechnen.
Die Seiten a und b des rechtwinkligen Dreiecks (Katheten) entsprechen dem Radius r.
Für den Satz des Pythagoras gilt daher:
a² + b² = c²
5² + 5² = c²
50 = c² | √
7,07 cm = c
Antwort: Die Seitenlänge des Quadrats beträgt 7,07 cm.
Fläche Quadrat
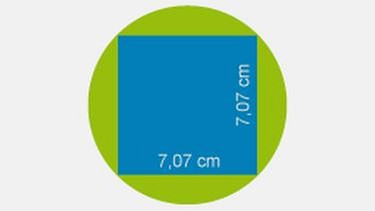
Allgemeine Formel (Flächeninhalt Quadrat):
A (Quadrat) = a · a
A (Quadrat) = 7,07 · 7,07
A (Quadrat) ≈ 50 cm²
Antwort: Das Quadrat hat einen Flächeninhalt von 50 cm².
Gefärbte Fläche
Gefärbte Fläche = Fläche Kreis - Fläche Quadrat
Gefärbte Fläche = 78,5 cm² - 50 cm² = 28,5 cm²
Antwort: Die gefärbte Fläche beträgt 28,5 cm².
