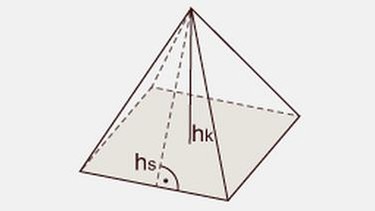
Eine gerade Pyramide mit quadratischer Grundfläche A = 2304 cm² hat eine Oberfläche von 6144 cm².
Berechne:
a. die Mantelfläche b. die Seitenhöhe c. die Körperhöhe
a. Mantelfläche
Mantelfläche = Oberfläche - Grundfläche M = 6144 cm² - 2304 cm² M = 3840 cm²
Antwort: Die Mantelfläche beträgt 3840 cm².
b. Seitenhöhe
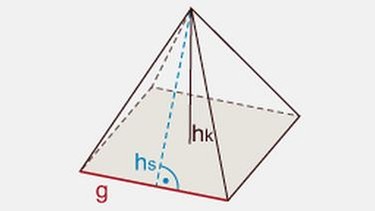
Länge der Grundseite:
A (Quadrat) = a² 2304 = a² | √ 48 cm = a
Hinweis: Bei einem Dreieck wird die Grundseite meist mit g bezeichnet. Sie entspricht der eben berechneten Seite a.
Die Mantelfläche der Pyramide besteht aus vier Dreiecken:
Mantelfläche = 4 · Dreiecksfläche Mantelfläche = 4 · Grundseite g · Höhe s : 2 M = 4 · (g · h) : 2 3840 = 4 · (48 · h) : 2 3840 = 192 · h : 2 3840 = 96 · h | : 96 40 = h
Antwort: Die Seitenhöhe s beträgt 40 cm.
c. Körperhöhe
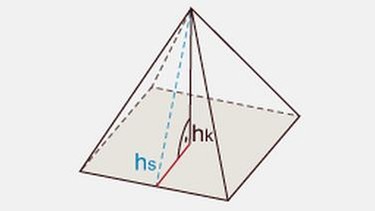
Satz des Pythagoras: a² + b² = c²
Die Länge der Grundseite a hast du in Schritt b berechnet (a = 48 cm). Im abgebildeten rechtwinkligen Dreieck findest du sie als Kathete wieder, allerdings halbiert bis zum Mittelpunkt (also: a = 24 cm).
Die Seitenhöhe der Pyramide (blaue Linie) ist gleichzeitig die Hypotenuse des eingezeichneten rechtwinkligen Dreiecks (c = 40 cm):
