Mathematik Anwendungen quadratischer Funktionen
Durch die Anwendungen quadratischer Gleichungen lassen sich einige Sachprobleme lösen. Welche - das sehen Sie am konkreten Beispiel in dieser Folge von Telekolleg Mathematik.
Der Inhalt dieser Lektion schließt direkt an die Berechnung der Nullstellen einer quadratischen Funktion in Lektion 5 an.
Wenn man weiß, wie die Nullstellen der quadratischen Funktion y = x2 + b · x + c berechnet werden, dann kann man auch die Lösungen der quadratischen Gleichung x2 + p · x + q = 0 bestimmen.
Übersicht über Lektion 6
6.1 Die Lösungen der quadratischen Gleichung
x2 + p · x + q = 0
Die Lösungen der quadratischen Gleichung
x2 + p · x + q = 0
sind Grundlage der Berechnungen für die gesamte Lektion 6.
6.2 Die allgemeine quadratische Gleichung
a · x2 + b · x + c = 0
Die allgemeine quadratische Gleichung
a · x2 + b · x + c = 0 lässt sich auf die in 6.1 erarbeiteten Grundlagen zurückführen.
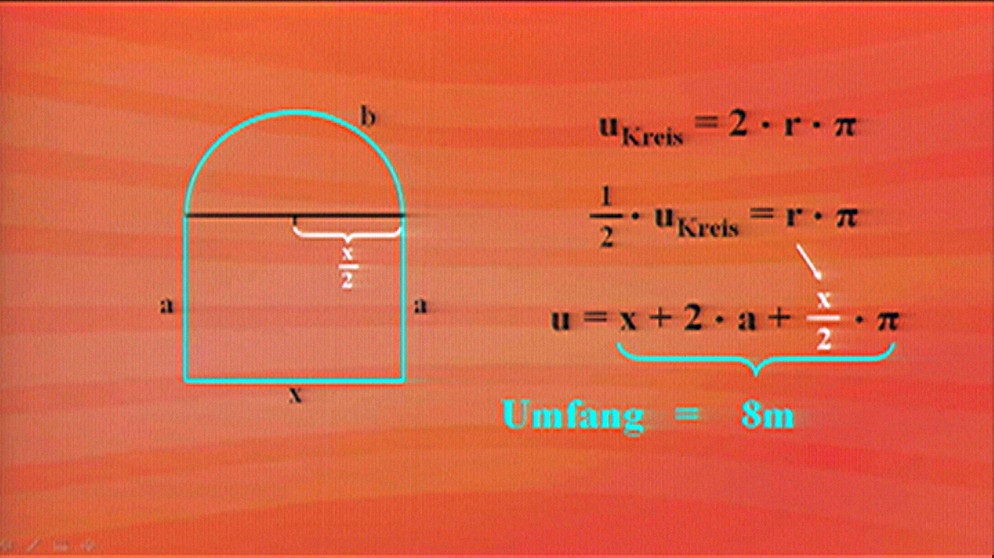
6.3 Anwendungen quadratischer Gleichungen
Durch die Anwendungen quadratischer Gleichungen
lassen sich einige Sachprobleme lösen.
Die komplette Sendung sehen Sie oben als Video - klicken Sie bitte auf den Pfeil.