Oben können Sie das Video der komplettten Sendung noch einmal ansehen - klicken Sie auf den Pfeil.

Kolleggruppe, nach Lebensalter geordnet

Als Beispiele werden zuerst die Daten der Telekolleggruppe aus der 1. Folge herangezogen. Zunächst stellen sich die Kollegiatinnen und Kollegiaten gemäß der Reihenfolge ihres Lebensalters auf. Als weiteres Beispiel einer anderen Rangordnung stellen sich die Teilnehmer dann gemäß ihrer Körpergröße auf.

Rangwertliste und Zentralwert

Männer der Kolleggruppe, nach Körpergröße geordnet

Die aus der ersten Folge schon bekannten Merkmalsausprägungen, die in einer Urliste festgehalten wurden, können nun entsprechend den oben genannten Beispielen geordnet werden, man spricht dann von einer Rangwertliste. Als weitere Verfeinerung der Rangwertliste wurden schließlich die männlichen Kollegiaten gemäß ihrer Körpergröße aufgestellt. Die Differenz zwischen dem größten und dem kleinsten Mann liefert die Spannweite, hier sind es 30 cm.

Frauen der Kolleggruppe, nach Körpergröße geordnet, mit Median

In einer weiteren Aufstellung nach Größe, hier die der Damen, wird der Begriff Median oder Zentralwert erläutert, es ist der Mittelwert aus der größten und kleinsten Körpergröße.

Arithmetisches Mittel und Zentralwert

Ermittlung des arithmetisches Mittels aus der Urliste - bitte klicken Sie auf die Lupe

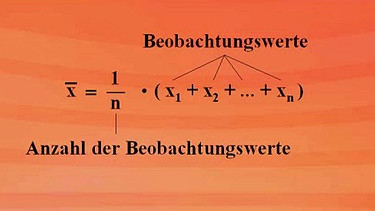
Davon unterschieden werden muss das sogenannte arithmetische Mittel, hier also die Summe der Körpergrößen geteilt durch die Anzahl der zugehörigen Personen. Allgemein formuliert ist das arithmetische Mittel die Summe der Beobachtungswerte geteilt durch die Anzahl der Beobachtungswerte. Oben stehendes Bild zeigt die Formel - klicken Sie bitte auf die Lupe.

Arithmetisches Mittel von Merkmalsgruppen - bitte klicken Sie auf die Lupe

Merkmale können in Merkmalsgruppen zusammengefasst werden. Sind die absoluten Häufigkeiten n_i bestimmter Merkmalsausprägungen a_i bekannt, so ist das arithmetische Mittel "x quer“ die Summe der Produkte aus den Merkmalsausprägungen a_i und den relativen Häufigkeiten h (a_i) von i = 1 bis k, wenn k die Anzahl der Merkmalsausprägungen ist.

Häufigkeit der Merkmalsgruppen - bitte klicken Sie auf die Lupe

Ein Beispiel mit 4 Merkmalsausprägungen verdeutlicht die Anwendung der Formel. Werden die Werte aus der Tabelle in die Formel eingesetzt, so ergibt sich ein Wert von "x quer“ zu 173 cm.

Berechnung des arithmetischen Mittels der Merkmalsgruppen - bitte klicken Sie auf die Lupe

Die Berechnung des arithmetischen Mittels der Merkmalsgruppen sehen Sie links im Bild - bitte klicken Sie auf die Lupe.

Median und arithmetisches Mittel - bitte klicken Sie auf die Lupe

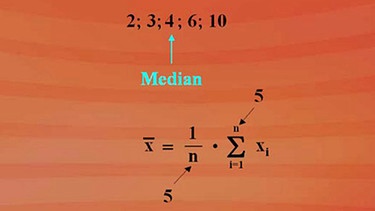
Ein weiteres Beispiel mit einer beliebig gewählten Rangwertliste 2; 3; 4; 6; 10 verdeutlicht nochmals den Unterschied zwischen dem Median und dem arithmetischen Mittel. Vergleichen Sie dazu neben stehendes Bild, bitte klicken Sie auf die Lupe.

Rechenbeispiel

An dem gewählten Beispiel lässt sich auch zeigen, dass die Summe der Differenzen aus Beobachtungswerten und arithmetischem Mittel wirklich Null ist.

Rechnerische Bestimmung des Zentralwerts für ungeradzahlige Beobachtungswerte

Der Median x_med oder Zentralwert z wurde bisher nur durch Abzählen ermittelt. Zwei Formeln liefern die mathematischen Mittel, ihn jeweils auch zu berechnen: Für eine ungerade Zahl von Beobachtungswerten gilt x_med = x von (n + 1)/2, für das gewählte Beispiel also x_med = x₃.

Rechnerische Bestimmung des Zentralwerts für geradzahlige Beobachtungswerte - klicken Sie bitte auf die Lupe

Bei einer geraden Anzahl von Beobachtungswerten muss eine andere Formel angewendet werden. Als Beispiel wird die bereits bekannte Rangwertfolge um die Zahl 13 ergänzt. Die Formel lautet diesmal: Der Zentralwert z bzw. x_med ist ein halb mal Klammer auf x von n halbe plus x von n halbe plus 1, Klammer zu. In dem gewählten Beispiel ergibt sich z = x_med = 5.

Modalwert, Verteilungen

Drei mögliche Arten der Verteilung von Beobachtungswerten - klicken Sie bitte auf die Lupe

Ein weiteres Lagemaß ist der "Modalwert“. Er ist der Wert, der bei vorliegenden Daten am häufigsten vorkommt. Werden alle drei dargestellten Lagemaße berechnet, lassen sich aus deren Vergleich zusätzliche Informationen zur Verteilung der untersuchten Daten gewinnen. Wenn x quer für arithmetisches Mittel ungefähr gleich zu x_med für Median oder Zentralwert und nochmals ungefähr gleich zu x_mod für Modalwert ist, ergibt sich eine symmetrische Verteilung. Ist das arithmetische Mittel jedoch größer als der Zentralwert und der wieder größer als der Modalwert, haben wir keine symmetrische Verteilung mehr, sondern eine sogenannte rechtsschiefe Verteilung. Verhalten sich die drei Werte umgekehrt, ist also das arithmetische Mittel der kleinste Wert und der Zentralwert kleiner als der Modalwert, ergibt sich eine linksschiefe Verteilung.

Übersicht über die wichtigsten Lagemaßbegriffe

Die wichtigsten Lagemaßbegriffe - klicken Sie bitte auf die Lupe

In einer Übersicht werden schließlich die wichtigsten Lagemaßbegriffe zusammengefasst. Vergleichen Sie dazu neben stehendes Bild, bitte klicken Sie auf die Lupe.

Anwendungsbeispiel

Rangwertliste der monatlichen Ausgaben mit dem Modalwert - klicken Sie bitte auf die Lupe

Die Lagemaßbegriffe werden nun auf die Daten aus einer Umfrage angewendet, bei der elf Studenten Auskunft über ihre monatliche Ausgaben gaben. Die Daten aus der Urliste werden zunächst in einer Rangwertliste geordnet.

Rangwertliste der monatlichen Ausgaben mit dem Zentralwert bzw. Median - klicken Sie bitte auf die Lupe

Aus der unmittelbaren Beobachtung ergibt sich ein Modalwert von 750 €. Der Zentralwert dagegen errechnet sich zu 800 €. Vergleichen Sie dazu oben- und nebenstehendes Bild, bitte klicken Sie auf die Lupe.

Rangwertliste mit dem Durchschnittswert aller Ausgaben - klicken Sie bitte auf die Lupe

Der Durchschnittswert aller Ausgaben schließlich lässt sich zu 981,82 € bestimmen. Es handelt sich also um eine "rechtsschiefe Verteilung", die auf den "Ausreißer" von 2800 € zurückzuführen ist.