GRIPS Mathe 14 Berechnung der Tageszinsen

Ein Fachgeschäft bietet ein Notebook für 1750 € an. Zahlbar ist es erst in 175 Tagen bei einem Zinssatz von 7,5 %. Welcher Betrag muss für das Notebook nach Ablauf der Frist insgesamt bezahlt werden?
- Das Kapital beträgt 1750 €
- Der Zinssatz ist mit 7,5 % p. a. angegeben. Die Abkürzung p. a. (per anno) stammt aus der lateinischen Sprache und bedeutet: für ein Jahr.
- Der Kredit wird für 175 Tage (= Laufzeit) gewährt.
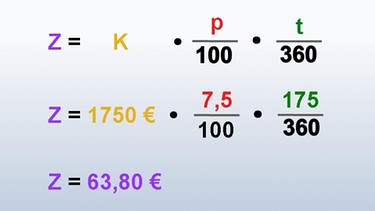
Berechnung der Tageszinsen mit der Formel
- Zu der bereits bekannten Zinsformel kommt wieder der Faktor Zeit hinzu. In diesem Fall allerdings Tage.
- Bei der Zinsrechnung rechnet man mit 360 Tagen im Jahr, deshalb taucht beim Faktor Zeit auch die Zahl 360 im Nenner auf.
- 360/360 wären wieder ein Ganzes, das heißt die Zinsformel würde für ein Jahr gelten.
- In unserem Beispiel fallen jedoch nur für 175 Tage Kreditzinsen an. Das bedeutet der Anteil der Kreditzinsen beträgt auch nur 175/360.
- Nach dem Einsetzen und dem Ausmultiplizieren ergibt sich ein Zinsbetrag in Höhe von 63,80 €.
- Damit würde das Notebook insgesamt 1813,80 € (1750 € + 63,80 €) kosten.
Berechnung der Tageszinsen mit dem Dreisatz
Die Tageszinsen lassen sich auch mit dem Dreisatz berechnen. Auch hier sind wieder zwei Dreisatzrechnungen notwendig.
- Das Kapital entspricht wieder 100 %.
- Über den Zwischenschritt 1% können die Jahreszinsen bei einem Zinssatz von 7,5 % berechnet werden.
- Ergebnis des ersten Dreisatzes: Die Zinsen für ein Jahr betragen in unserem Beispiel 131,25 €.
- Da die Zinsen nur für 175 Tage bezahlt werden müssen, ist ein zweiter Dreisatz notwendig, um von 360 auf 175 Tage zu kommen.
- Auch hier führt der Zwischenschritt über 1 Tag zur Lösung 63,80 €.
Hinweis
Rechne immer mit den Kommastellen im Taschenrechner weiter (hier: 0,364…). Ein Runden der Zwischenergebnisse könnte zu einem ungenauen Gesamtergebnis führen.