GRIPS Mathe 23 Prismen
Nicola und Felix wollen Leon, dem Kraftprotz der Klasse, einen Pokal für seine Leistungen schenken. Dafür muss eine Verpackung her, in die der Pokal genau hineinpasst. Damit die Größe der Verpackung stimmt, lernen sie, wie sie die Oberfläche von Prismen berechnen können.

Bevor Nicola und Felix sich mit der Oberfläche von Geschenkverpackungen befassen, geben wir dir noch einmal einen Überblick über Prismen. In der Lektion Prisma und Zylinder hast du gelernt, was Prismen sind und wie man ihr Volumen berechnet. Auf dieser Seite kannst du noch einmal prüfen, wie gut du ihre Merkmale kennst:
Das solltest du über gerade Prismen wissen:
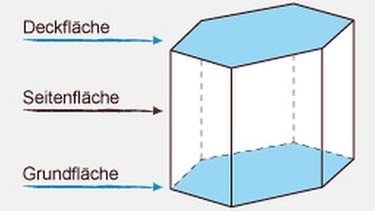
- Grundfläche und Deckfläche sind parallel zueinander.
- Grundfläche und Deckfläche sind deckungsgleiche Vielecke.
- Die Seitenflächen stehen senkrecht auf der Grundfläche.
- Die Seitenflächen sind Rechtecke.
Beispiele für gerade Prismen
Es gibt viele verschiedene Prismen. Einige der wichtigsten siehst du hier:
Prismen mit verschiedenen Grundflächen
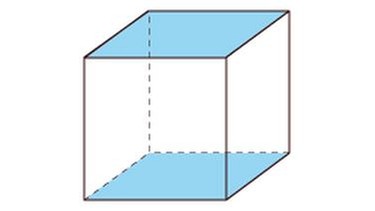
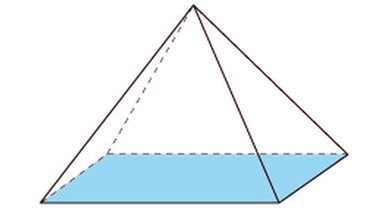
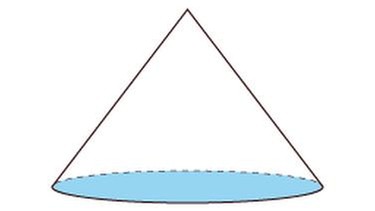
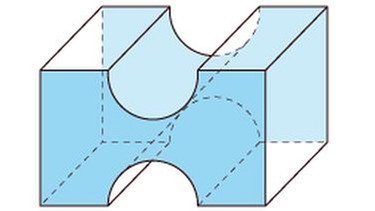
Das sind keine Prismen
Nun noch einige Beispiele für geometrische Körper, die keine Prismen sind. Klicke dich durch die verschiedenen Körper und erfahre, warum sie keine Prismen sind.