GRIPS Mathe 26 Flächen
Wenn du mit offenen Augen durch die Stadt gehst, kannst du viele geometrische Formen und Körper entdecken. Welche gibt es und wie lassen sie sich unterscheiden? Das erfährst du auf den folgenden Seiten.

Flächen können zum Beispiel Vierecke oder Dreiecke sein. Je nach Eigenschaft, sehen diese ganz unterschiedlich aus. Auf dieser Seite siehst du ihre wichtigsten Vertreter.
Vierecke
Viereck ist nicht gleich Viereck. Vierecke lassen sich anhand ihrer Winkelgrößen und der Länge ihrer Seiten unterscheiden. Außerdem gibt es Vierecke mit parallel und nicht parallel verlaufenden Seiten. Hier einige Beispiele:
Vierecke und ihre Eigenschaften
Quadrat

Quadrat
Vier gleich lange Seiten
Die gegenüberliegenden Seiten sind parallel.
Alle Winkel betragen 90°
Rechteck

Rechteck
Die gegenüberliegenden Seiten sind gleich lang und parallel.
Alle Winkel betragen 90°.
Symm. Trapez
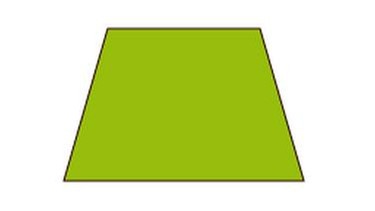
Symmetrisches Trapez
Zwei der Seiten sind parallel.
Die beiden anderen Seiten (Schenkel) sind gleich lang.
Trapez
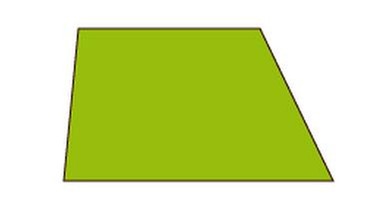
Trapez
Zwei gegenüberliegende Seiten sind parallel.
Parallelogramm

Parallelogramm
Gegenüberliegende Seiten sind parallel und gleich lang.
Gegenüberliegende Winkel sind gleich groß.
Raute

Raute
Alle vier Seiten sind gleich lang.
Gegenüberliegende Seiten sind parallel.
Gegenüberliegende Winkel sind gleich groß.
Symm. Drache

Symmetrischer Drache
Je zwei benachbarte Seiten sind gleich lang.
Zwei gegenüberliegende Winkel sind gleich groß.
Dreiecke
Auch bei Dreiecken gibt es Unterschiede. Ein Dreieck kann zum Beispiel rechtwinklig, spitzwinklig oder stumpfwinklig sein. Was das bedeutet und wie solche Dreiecke aussehen, erfährst du hier:
Dreiecke und ihre Eigenschaften
Stumpfwinklig
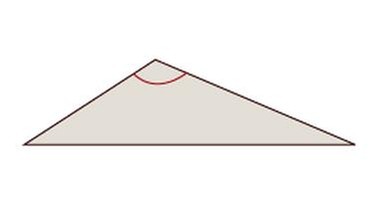
Stumpfwinklige Dreiecke
Ein Winkel ist größer als 90°.
Rechtwinklig

Rechtwinklige Dreiecke
Ein Winkel beträgt genau 90°.
Spitzwinklig
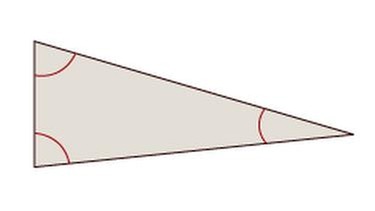
Spitzwinklige Dreiecke
Alle Winkel sind kleiner als 90°.
Gleischenklig
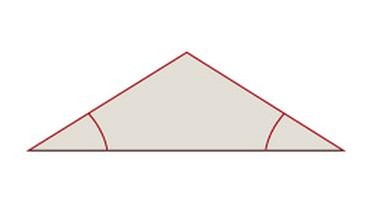
Gleichschenklige Dreiecke
Zwei Seiten (Schenkel) sind gleich lang.
Zwei Winkel (Basiswinkel) sind gleich groß.
Gleichseitig

Gleichseitige Dreiecke
Alle drei Seiten sind gleich lang.
Alle drei Winkel betragen 60°.
