GRIPS Mathe 27 Achsenspiegelung
Faltest du ein Papier mit einem Farbklecks, dann ensteht so eine ähnliche Figur. Diese Abbildung ist achsensymmetrisch:
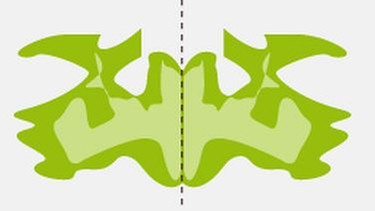
Eine achsensymmetrische Figur besteht aus zwei Teilen, die beim Falten genau aufeinander passen.
Die Faltachse wird als Symmetrie- oder Spiegelachse bezeichnet (hier gestrichelt eingezeichnet).
Im Alltag findest du viele solcher symmetrischen Figuren:
Symmetrische Figuren
Schmetterling
Dieser Schmetterling ist achsensymmetrisch. Wenn du seine Flügel aufeinanderklappst, sind sie genau deckungsgleich.
Kathedrale
Auch das Bild dieser Kathedrale ist achsensymmetrisch.
Zähne
Und sogar beim Menschen gibt es Achsensymmetrie - zum Beispiel bei den Zähnen.
Achsensymmetrie
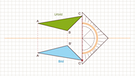
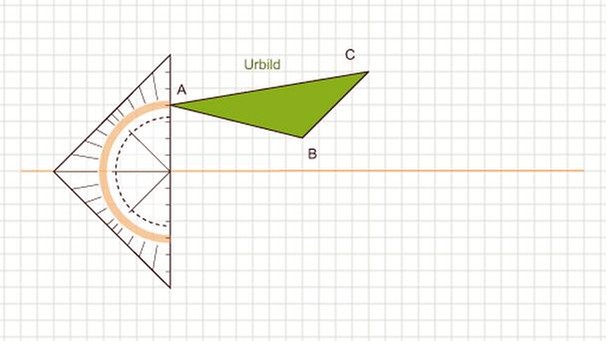
- Bei einer Achsenspiegelung wird eine Ausgangsfigur (Urbild) in eine Bildfigur abgebildet.
- Bezeichnung der Urpunkte: A, B, C, …
- Bezeichnung der Bildpunkte: A', B', C', … (sprich: A Strich)
- Punkt und Bildpunkt sind von der Symmetrieachse gleich weit entfernt.
- Die Verbindungslinie von Urpunkt und Bildpunkt steht senkrecht auf der Symmetrieachse und wird von dieser halbiert.
- Längen und Winkel der Ausgangsfigur bleiben in der Bildfigur unverändert.
- Urbild und Bild sind deckungsgleich.
Damit du dir das besser vorstellen kannst, hier ein Beispiel: Gespiegelt werden soll das Ausgangsdreieck ABC an der Symmetrieachse. Heraus kommt das Spiegeldreieck A'B'C':
Du möchtest das Dreieck ABC an der Symmetriachse spiegeln. Dazu beginnst du mit Punkt A. Lege das Geodreieck mit der Mittellinie so auf die Symmetrieachse, dass die Grundlinie des Geodreiecks durch den Punkt A läuft.