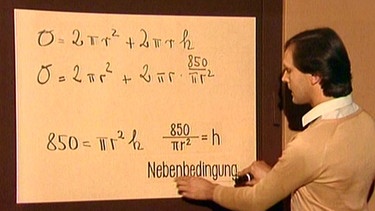Extremwertaufgaben 1 Praktisches Beispiel: Konservendosen
Ist Ihnen schon einmal aufgefallen, dass Konservendosen fast immer das gleiche Verhältnis von Durchmesser und Höhe haben? Warum ist das so? Um die Antwort zu finden, soll zum Schluss nochmals eine geometrische Aufgabe gelöst werden:
Sieht man sich im Lebensmittelhandel um, so findet man für die gängige Konservendose mit 850 ml Inhalt nur sehr selten Formen, wie die beiden gelben Modelle, die gängige Ausführung zeigt die handelsübliche Blechdose. Warum ist das so?
Gesucht: die minimale Oberfläche
Die Hersteller wollen bei solch einem Massenartikel bei gegebenem Volumen die Oberfläche dieses Zylinders möglichst klein halten, um Material zu sparen. Gesucht wird also die minimale Oberfläche Ominimal .
Der Zylinder setzt sich aus Boden und Deckel jeweils mit dem Radius r und der Fläche FKreisscheibe = π r2 zusammen sowie aus dem rechteckigen Zylindermantel mit der Fläche FMantel = 2π r·h . Die gesamte Oberfläche kann also durch die Formel O = 2·π r2 + 2π r·h berechnet werden.
Nebenbedingung
Hier tauchen allerdings zwei Variable auf, r und h, so dass h durch einen anderen Zusammenhang ausgedrückt werden muss. r und h sind auch noch durch die Formel für das Volumen verknüpft, V = π·r2·h, in diesem speziellen Fall mit V = 850 gilt also 850 = π·r2·h bzw. h = 850/ π·r2. Setzt man h in die Gleichung O = 2·π r2 + 2π r·h ein, so ergibt sich für die Oberfläche in Abhängigkeit von r die Funktion 2·π r2 + 2π r·850/π r2.
Den zweiten Zusammenhang zwischen r und h, h = 850/ π·r2, bezeichnet man als Nebenbedingung.
Testen Sie Ihr Wissen!