Die Integralfunktion Weiteres Rechenbeispiel
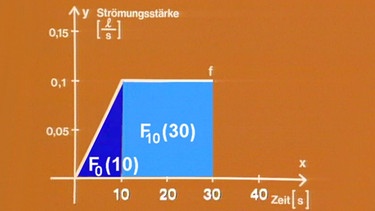
In einem weiteren Versuch lässt man die Pumpenleistung erst langsam bis zum Wert 0,1 l/s ansteigen, nach 10 s bleibt die Strömungsstärke dann konstant, bis die Pumpe nach insgesamt 30 s abgeschaltet wird.
Das Diagramm zeigt entsprechend erst einen Anstieg der Strömungsstärke bis 0,1 l/s und anschließend ab t1 = 10 s einen konstanten Wert bis t2 = 30 s . Das geförderte Volumen von t1 bis t2 entspricht der Fläche „F 10 von 30“, abgekürzt F10(30).
Das Volumen von 0 bis t1 entspricht der Fläche „F 0 von 10“, abgekürzt F0(10).
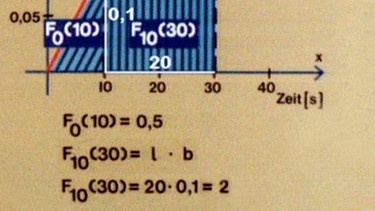
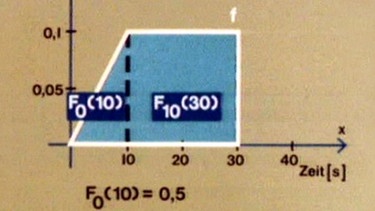
Aus den Zahlenwerten lassen sich die Teilflächen und dann auch die Gesamtfläche bzw. das geförderte Gesamtvolumen berechnen. Für die Dreiecksfläche gilt: F0(10) = 0,5 · g · h = 0,5·10·0,1 = 0,5 .
Die Fläche des Rechtecks ergibt sich zu: F10(30) = l · b = 20·0,1 = 2 .
Die Gesamtfläche ist die Summe der Teilflächen: F0(30) = F0(10) + F10(30) = 0,5+2 = 2,5 .
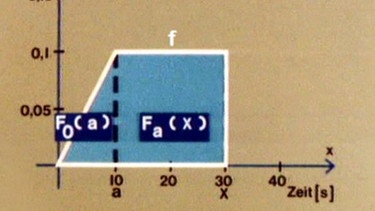
Setzt man statt der speziellen Werte 10 und 30 die Platzhalter a und x in die gewonnene Funktionsgleichung ein, so ergibt sich F0(x) = F0(a) + Fa(x) .
Zwei Ergebnisse können wir festhalten:
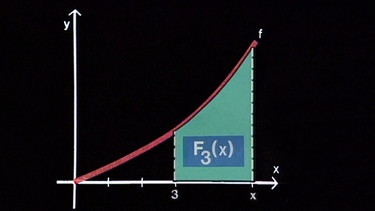
Die untere Grenze der Fläche muss nicht Null sein, ist sie beispielsweise 3, so hat die Fläche die Größe F3(x).
Teilflächen lassen sich einzeln berechnen und dann zu einer Gesamtfläche zusammensetzen. Diese Eigenschaft heißt Intervalladditivität.