Die Strömungsstärke kann auch negative Werte annehmen

Das Zeigerinstrument zeigt zunächst eine Zunahme der Strömungsstärke an, dann verbleibt sie auf einem konstanten Wert, nimmt dann wieder ab bis zum Wert Null und wird schließlich negativ, bevor sie schließlich erneut den Wert Null erreicht.

Durch die "negative" Strömungsstärke wurde das Flüssigkeitsvolumen im Auffangbehälter verkleinert.

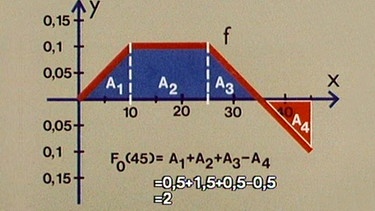
Das Diagramm zeigt, wie der Graph der Funktion durch die x-Achse in den negativen y-Bereich verläuft und schließlich wieder den Wert Null erreicht. Negative Strömungsstärke bedeutet, dass die Pumpe umgeschaltet wurde und dann Wasser vom Auffangbehälter zurück in das Vorratsgefäß gepumpt wurde. Aus dem 2 l-Vorratsgefäß wurden 0,5 l zurück gepumpt, der Flüssigkeitsspiegel ist nicht mehr am oberen Rand.

Die Teilfläche A4 entspricht einem Rücktransport der Flüssigkeit

Wie das Diagramm zeigt, lässt sich das Flüssigkeitsvolumen im Auffangbehälter durch die Addition der Teilflächen unter der Randfunktion berechnen, wobei A₄ ein negatives Vorzeichen bekommt, also subtrahiert wird: F₀(45) = A₁ + A₂ + A₃ – A₄, F₀(45) = 0,5+1,5+0,5-0,5 = 2 .

Fa(x) ist die Summe aus positiven und negativen Flächenabschnitten

Dieses Verfahren lässt sich allgemein auf beliebige Funktionen mit positiven und negativen Abschnitten übertragen. Man bildet die Summe der positiven Abschnitte (z.B. A₁ + A₃) und die Summe der negativen Abschnitte (z.B. A₂ + A₄) und subtrahiert anschließend (A₂ + A₄) von (A₁ + A₃), also F_a(x) = (A₁ + A₃) – (A₂ + A₄) .

Fa(x) ist die Differenz der Summe der Teilflächen oberhalb und der Summe der Teilflächen unterhalb der x-Achse

Allgemein formuliert lautet die Definition:

F_a(x) = (Summe aus den Inhalten der Teilflächen über der x-Achse) -  (Summe aus den Inhalten der Teilflächen unter der x-Achse).

Fa(x) wird als Integralfunktion von a bis x der Funktion f(t) bezeichnet.

Die Funktion F_a(x) erhält in dieser allgemeinen Bedeutung die Bezeichnung Integralfunktion mit der Schreibweise F_a(x) = _a∫^x f(t) dt.

Das Integralzeichen ∫ ist aus dem Buchstaben „langes s“ der sog. Deutschen Schrift als Abkürzung für das Wort Summe, lateinisch summa, entstanden. Diese symbolische Schreibweise von Integralen geht auf den Mathematiker Gottfried Wilhelm Leibniz zurück.

Die Schreibweise f(t) dt deutet an, dass sich die Integraloperation aus Streifen der infinitesimalen Breite dt zur Fläche unter der Funktion summiert. Von dem Mathematiker Johann Bernoulli schließlich stammt die Bezeichnung calculus integralis, Integralrechnung, für diese Art der Summenberechnung.