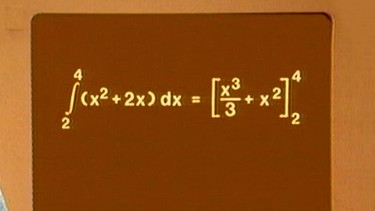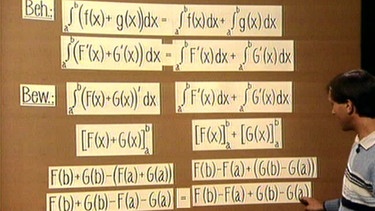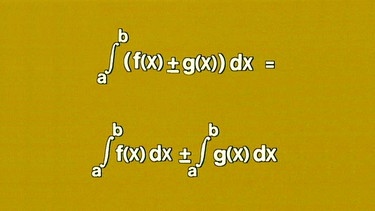Telekolleg - Integralrechnung Ableitung der Integrationsregeln
Im Rückblick auf die vorherige Folge wird zunächst das Integrieren einer Funktion wiederholt, die aus der Summe einer quadratischen und einer linearen Funktion besteht. Anschließend finden wir die Regel für das Integrieren der Summe oder Differenz zweier Funktionen.
Integrieren der Summe einer quadratischen und einer linearen Funktion
Nach dem Integrieren wurde zunächst die obere Grenze - hier 4 - in die Summenfunktion eingesetzt und berechnet, dann die untere Grenze - hier 2 - ebenfalls in die Summenfunktion eingesetzt und berechnet, und dann die Differenz aus oberer und unterer Grenze ermittelt.
Integralfunktion mit oberer und unterer Grenze
Man hätte aber zunächst die obere Grenze und die untere Grenze in den ersten Summanden - hier x3/3 - einsetzen und dann die Differenz bilden können, dann die gleiche Prozedur auf den zweiten Summanden - hier x2 - anwenden und schließlich die Summe der beiden Summanden bilden können.
Die oben beschriebene Operation lässt sich allgemein so formulieren:
Das Integral der Summe zweier Funktionen ist gleich der Summe der Integrale der beiden einzelnen Funktionen, a∫b(f(x) + (g(x))dx = a∫b(f(x)dx + a∫b(g(x)dx
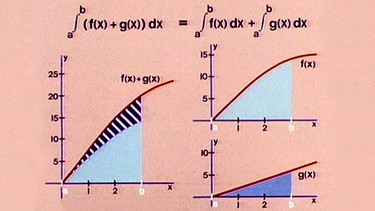
Die Summe der Flächen unter den Randfunktionen rechts ist gleich der Summe der Fläche unter der Randfunktion links.
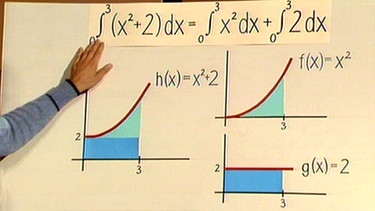
Dass diese Überlegung plausibel ist, lässt sich an einem geometrischen Beispiel zeigen: Die Summe der Fläche von 0 bis 3 unter der Randfunktion f(x) = x2 und der Fläche unter der Randfunktion g(x) = 2 ist gleich der Summe der Fläche von 0 bis 3 unter der Randfunktion f(x) = x2 + 2.
Grafisches Beispiel der ddition zweier Flächen unter Funktionen mit etwas komplizierterem Verlauf
Ein weiteres grafisches Beispiel der Addition zweier Flächen unter Funktionen mit etwas komplizierterem Verlauf zeigt aber, dass hier der Nachweis der Gleichheit der Summe der Fläche unter den Einzelfunktionen und der Fläche unter der Summenfunktionen nicht durch bloßen Augenschein zu erbringen ist. Ob nämlich die schraffierte Fläche unter der Randfunktion f(x) + g(x) gleich der Summe der Flächen unter den Funktionen f(x) und g(x) ist, lässt sich wegen der gekrümmten Form nicht sagen.
Beweisführung durch die bekannten Regeln für das Differenzieren
Der Beweis für die Behauptung a∫b(f(x) + g(x))dx = a∫bf(x)dx + a∫bg(x)dx lässt sich dadurch erbringen, dass man auf die bekannten Regeln für das Differenzieren zurückgreift. Dazu werden f(x) und g(x) durch die Ableitungen ihrer Stammfunktionen, nämlich F’(x) und G’(x), ersetzt. Werden nun die Summenfunktion von F’(x) und G’(x) und die Summe der Funktionen F’(x) und G’(x) jeweils zwischen den Grenzen a und b integriert, so erhält man in beiden Fällen das gleiche Ergebnis.
0∫4
Regel für das Integrieren der Summe oder Differenz zweier Funktionen
Den gleichen Beweis kann man führen, wenn nicht die Summe (F(x) + G(x))’, sondern die Differenz (F(x) - G(x))’ integriert wird. Somit ist allgemein bewiesen:
a∫b(f(x) +/- g(x))dx = a∫bf(x)dx +/- a∫bg(x)dx
Die Regel für das Integrieren einer Funktion mit einem konstanten Faktor soll plausibel gemacht werden.
Als weitere Integrationsregel wird gezeigt, dass ein Faktor vor einer Funktion (f(x), die integriert werden soll, vor das Integral gestellt werden kann, ohne dass sich das Ergebnis ändert, im Beispiel 0∫4(x/4)dx = (1/4) 0∫4x dx .