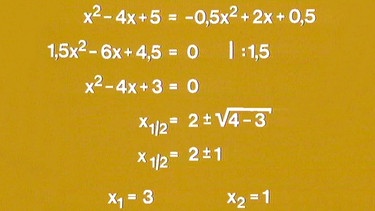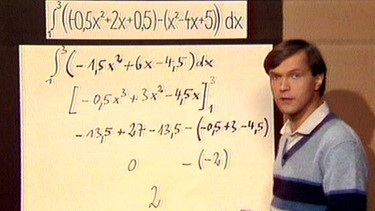Telekolleg - Integralrechnung Rezept zur Flächenberechnung
Wir formulieren nun ein Rezept zur Flächenberechnung und berechnen ein weiteres Beispiel aus der Praxis.
Ob eine Integralfunktion positive und negative Abschnitte besitzt, erkennt man an den Nullstellen.
Für Flächenberechnungen addiert man die Beträge der Integrale.
An der Nullstelle wechselt (meist, aber nicht immer) das Vorzeichen. Man berechnet dann Teilfläche A von der unteren Grenze a bis zur Nullstelle und Teilfläche B von der Nullstelle bis zur oberen Grenze b. Die Teilflächen A und B werden nun addiert.
Rezept zur Flächenberechnung
Rezept zur Flächenberechnung bei einer Randfunktion mit einer oder mehreren Nullstellen
Das Rezept zur Flächenberechnung bei einer Randfunktion mit einer oder mehreren Nullstellen lautet also: Nullstellen bestimmen - Teilintegrale bilden - Beträge der Teilintegrale addieren.
Praktisches Beispiel
Das Grundstück zwischen Schienenstrang und Straße soll berechnet werden.
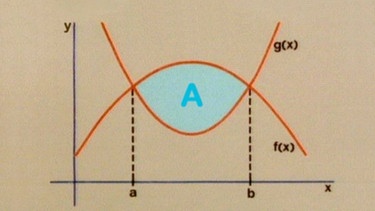
Beim nächsten Beispiel aus der Praxis kreuzen sich eine bogenförmig verlaufende Eisenbahnlinie und eine ebenfalls bogenförmig verlaufende Straße zweimal. Wegen der Lärmbelastung will der Grundbesitzer das Grundstück zwischen Bahngleisen und Straße verkaufen und lässt die Fläche berechnen.
Die Fläche A wird von den Schnittpunkten der beiden Graphen bei a und b begrenzt.
Die zu berechnende Fläche A befindet sich nun nicht mehr zwischen einem Graphen und der x-Achse, sondern zwischen den Graphen zweier Funktionen f(x) und g(x). Wie die Graphik zeigt, wird diese Fläche von den Schnittpunkten der beiden Graphen bei x1 = a und x2 = b begrenzt.
Die Differenzfläche A ist gleich der Differenz der Integrale zwischen a und b.
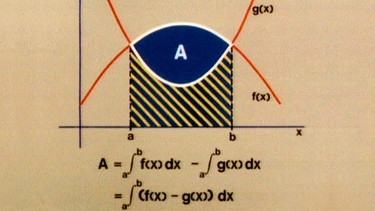
Zur Bestimmung der Fläche A berechnet man zunächst die Fläche zwischen der x-Achse und der Randfunktion f(x) von a bis b, also A1 = a∫bf(x) dx (in der Graphik die blau gefärbte Fläche) und subtrahiert davon die Fläche A2 = a∫bg(x) dx (in der Graphik die gelb schraffierte Fläche).
Wir erhalten dann die Differenzfläche A = a∫bf(x) dx - a∫bg(x) dx = a∫b(f(x) - g(x)) dx.
Den Randfunktionen werden Zahlenwerte zugeordnet.
Den Randfunktionen werden nun Zahlenwerte zugeordnet: f(x) = -0,5x2+ 2x + 0,5 und (g(x) = x2- 4x + 5.
Berechnung der Grenzen a und b
Die x-Werte der Schnittpunkte a und b erhalten wir durch Gleichsetzen: f(x) = g(x) => -0,5x2+ 2x + 0,5 = x2- 4x + 5. Durch Umstellen, Zusammenfassen und Kürzen ergibt sich die quadratische Gleichung x2- 4x + 3 = 0. Als Lösung dieser Gleichung erhalten wir x1 = 3 und x2 = 1.
Die Integralfläche A hat den Wert 2 (Flächeneinheiten)
Damit lässt sich nun die Integralfläche A berechnen: A = 1∫3(-0,5x2 + 2x + 0,5 - (x2 - 4x + 5)) dx . Durch Zusammenfassen erhalten wir daraus A = 1∫3 (-1,5x2 + 6x - 4,5) dx . Das folgende Integrieren ergibt die Stammfunktion A = [-0,5x³+ 3x2 - 4,5x]13.
Setzen wir die Grenzen 1 und 3 in die Gleichung ein, so erhalten wir A = -13,5 + 27 - 13,5 -(0,5 + 3 - 4,5) = 2 .