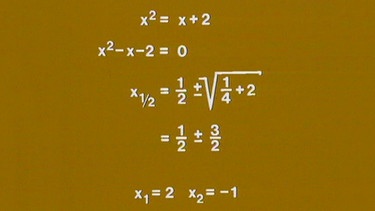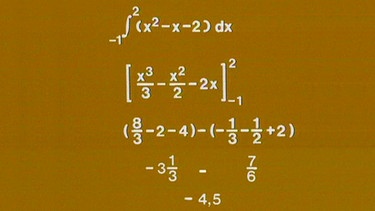Telekolleg - Integralrechnung Flächen zwischen Funktionsgraphen
Wir beschreiben nun ein Rezept für die Berechnung von Flächen zwischen Funktionsgraphen.
Die Fläche zwischen dem Graphen einer Parabel und einer Geraden soll berechnet werden.
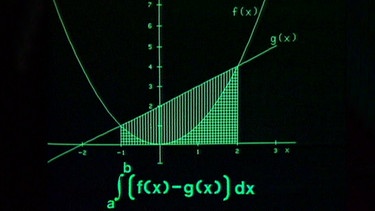
Als weiteres Beispiel soll nun die Fläche zwischen den Graphen der Funktionen f(x) = x2 und g(x) = x + 2 bestimmt werden. Das zugehörige Integral lautet dann a∫b(x2- x - 2).
Berechnung der Integrationsgrenzen
Die x-Koordinaten der Schnittstellen der beiden Graphen erhalten wir wieder durch Gleichsetzen der Funktionen: x2 = x + 2. Daraus ergibt sich die quadratische Gleichung x2 - x - 2 = 0 mit den Lösungen x1 = 2 und x2 = -1.
Berechnung des Integrals
Die gesuchte Fläche A hat dann die Größe A = -1∫2(x2- x - 2) = [x3/3 - x2/2 - 2x]-1 2 = (8/3 - 2 - 4) - (-1/3 - 1/2 + 2) = -4,5.
Die Differenz des kleineren Integrals von f(x) und des größeren Integrals g(x) besitzt ein negatives Vorzeichen
Der negative Zahlenwert erklärt sich dadurch, dass die Fläche unter der Parabel f(x) = x2 (waagerecht schraffierte Fläche) kleiner ist als die Fläche unter der linearen Funktion g(x) = x + 2, die in diesem Fall größer ist.
Für die Flächenberechnung zwischen Graphen bestimmt man daher immer den Betrag des Integrals (wie schon im 1. Beispiel dieses Beitrags), also A = | -1∫2(x2- x - 2) | = 4,5.
Rezept für die Berechnung von Flächen zwischen Funktionsgraphen
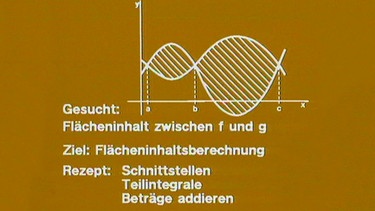
Rezept für die Berechnung von Flächen zwischen Funktionsgraphen
Zusammengefasst lautet also das Rezept für die Bestimmung von Flächen zwischen Funktionsgraphen: Schnittstellen berechnen (d.h. die Grenzen zwischen den Teilintegralen) – die Teilintegrale berechnen – die Beträge der Teilintegrale addieren.
Testen Sie Ihr Wissen!
