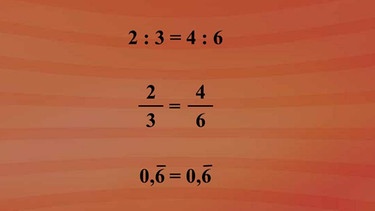6. Proportionalitäten 6.1. Was sind Proportionen?
Bei proportionalen Größen ist die Veränderung der einen Größe mit der gleichen Veränderung der anderen Größe verbunden. Man kann das schön an einer Zapfsäule beobachten. Aber beginnen wir mit einem einfachen Beispiel:
Ein Beispiel für Proportionen: Zwei verhält sich zu drei genauso wie vier zu sechs. In Brüchen geschrieben: zwei Drittel ist gleich vier Sechstel. Wer das nicht glaubt, kann seinen Taschenrechner nehmen und erhält für zwei geteilt durch drei: 0,6 Periode, sowie für vier geteilt durch sechs ebenfalls 0,6 Periode.
Was bedeutet proportional?
In Meyers Wissenslexikon kann man nachlesen, dass das Wort proportional für verhältnisgleich oder entsprechend steht. In der Mathematik sind Proportionen besondere Gleichungen. Man nennt nämlich eine Gleichung, die sich aus zwei Verhältnissen zusammensetzt, eine Verhältnisgleichung oder Proportion. Und eine Proportion, das wissen wir von den Gleichungen, ist dann wahr, wenn auf beiden Seiten das gleiche Verhältnis steht.
Der Begriff Proportionalität
Wenden wir uns dem Begriff Proportionalität zu. Bei proportionalen Größen ist die Veränderung der einen Größe mit der gleichen Veränderung der anderen Größe verbunden. Wird also die eine Größe verdoppelt oder halbiert, muss auch die andere Größe verdoppelt oder halbiert werden. Man kann das schön an einer Zapfsäule beobachten:
Beispiel für direkte Proportionalität - klicken Sie bitte auf die Lupe.
Der Preis für das getankte Benzin nahm mit der Literzahl gleichmäßig zu. Bei doppelter Benzinmenge ist auch der doppelte Preis zu zahlen. Eine Abhängigkeit zweier Beobachtungen in dieser Art nennt man direkte Proportionalität. Nebenstehend sehen Sie die beobachteten Werte in einer Tabelle zusammengestellt. Bei einem Liter zeigt das Kassenzählwerk 1,20 Euro. Bei 20 Liter 24,00 Euro und bei 40 Liter 48,00 Euro.
Zwei zusammengehörende Werte bilden jeweils ein Zahlenpaar. Wenn wir die Quotienten Preis durch Liter für die Zahlenpaare bilden, erhalten wir 1,20 Euro geteilt durch 1 Liter ist gleich 1,20 Euro pro Liter, oder 24 Euro geteilt durch 20 Liter ist gleich 1,20 Euro pro Liter, und so weiter.
Direkte Proportionalität
Wir sehen, dass es sich bei unseren Größenpaaren um quotientengleiche Zahlenpaare handelt. Quotientengleiche Zahlenpaare sind das Merkmal für eine direkte Proportionalität. Allgemein dargestellt:
Direkte Proportionalität:
Man schreibt a direkt proportional zu b mit einer Schlangenlinie als Zeichen für die direkte Proportionalität.
Grafische Darstellung
Grafische Darstellung
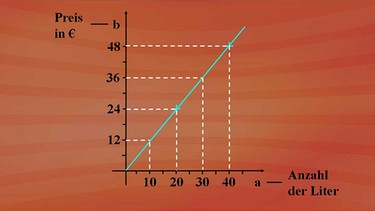
Das Ganze lässt sich auch grafisch darstellen. In einem Koordinatensystem wählen wir als Rechtswertachse die Anzahl der Liter, symbolisiert als Größe a und auf der Hochwertachse den dazugehörigen Preis, symbolisiert als Größe b.
Dann erhalten wir folgende eingezeichnete Punktepaare: 40 Liter auf der a-Achse gehören zu 48 Euro auf der b-Achse. 20 Liter auf der a -Achse gehören zu 24 Euro auf der b-Achse und so weiter. Wir können erkennen, dass die Punktepaare auf einer Geraden liegen, die durch den Nullpunkt des Koordinatensystems verläuft.
Auf dieser Geraden können wir jetzt ablesen, wie viele Liter Benzin ich zum Beispiel für zwölf Euro erhalte? Zehn Liter. Ich kann aber auch umgekehrt ablesen, was mich 30 Liter Benzin kosten - nämlich 36 Euro.
Rechnerische Darstellung: Proportionalitätsfaktor
Proportionalitätsfaktor - klicken Sie bitte auf die Lupe.
Aber auch rechnerisch könnten wir diese direkte Proportionalität in den Griff bekommen. Wir hatten doch die Quotienten Preis durch Liter gebildet und dabei den konstanten Wert 1,20 erhalten. Dieser konstante Faktor wird als Proportionalitätsfaktor bezeichnet, hier dargestellt als Variable c. Wir erhalten dann Proportionalitätsfaktor c ist gleich b (für den Betrag in Euro) durch a (für die Anzahl der Liter).
Der Zahlungsbetrag lässt sich dann stets über die Gleichung b ist gleich Proportionalitätsfaktor c mal a ermitteln. Für unser Beispiel mit den 30 Litern ergibt sich folgende Rechnung: b für Zahlungsbetrag ist gleich 1,20 Euro pro Liter für unseren Faktor c mal 30 Liter für a. Der Zahlungsbetrag lautet also 36 Euro.