6. Proportionalitäten 6.3. Umgekehrte Proportionalität
Die direkte Proportionalität kennen wir nun - fehlt noch die umgekehrte Proportionalität oder Antiproportionalität. Auch sie ist, am praktischen Beispiel betrachtet, leicht zu verstehen. Dieses Mal geht es um Kühe und ihr Futter.
Wenn die Merkmale für eine direkte Proportionalität quotientengleiche Größenpaare waren, müssen demnach die Merkmale für eine indirekte Proportionalität produktgleiche Größenpaare sein.
Um die Flächenmaßzahl 600 Quadratmeter zu erreichen, sind verschiedene Abmessungen möglich. Nimmt die Länge zu, so verringert sich die Breite. Wird die Breite reduziert, erhöht sich die Länge: Der doppelten Breite entspricht die halbe Länge; der vierfachen Länge ein Viertel der Breite. Somit gehören zu jeder indirekten Proportionalität produktgleiche Größenpaare.
Merksatz:
Zwei Größen a und b sind indirekt proportional, wenn dem n-fachen der Größe a der n-te Teil der Größe b zugeordnet ist.
Das Produkt der beiden Größen, die das Größenpaar bilden, gibt einen konstanten Wert.
Tabellendarstellung
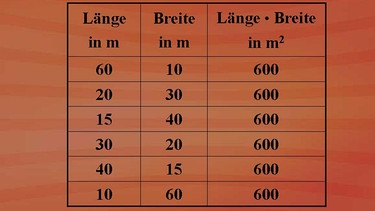
Schauen wir uns das mal für unsere Grundstückssuchende Familie in einer Tabellendarstellung an. In der ersten Spalte finden sich die Grundstückslänge in Meter, in der zweiten Spalte die Breite in Meter. Die Frau schlug vor: 60 Meter lang und 10 Meter breit. Das gibt 600 Quadratmeter. Diese 600 Quadratmeter sind festgelegt.
Bei 20 Meter Länge ergibt sich dann eine Breite von (20 mal wie viel gibt 600? 20 mal 30) 30 Meter Breite. Für 15 Meter Länge nach dem gleichen Prinzip: 40 Meter Breite ... Wir erkennen, dass es unendlich viele Möglichkeiten gibt.
Eines konnten wir in der Tabelle gut erkennen, die Größen Länge und Breite bilden produktgleiche Größenpaare. Wenn man eine Größe kennt, kann man über eine Division die andere dazugehörige Größe berechnen, da man ja den Produktwert als konstante Größe hat.
Grafische Darstellung
Die direkte Proportionalität hatte als grafische Darstellung eine Gerade durch den Koordinatenursprung. Wir untersuchen jetzt, welche Grafik sich für die indirekte Proportionalität, also für die produktgleichen Größenpaare, ergibt.
Dazu verwende ich unsere eben erstellte Tabelle für Länge und Breite des Grundstückes.
Die Rechtswertachse soll die Längenangaben enthalten und die Hochwertachse die Breitenangaben. Übertragen wir die Werte aus der Tabelle in unsere Grafik, so können wir erkennen, dass die Punkte sicherlich nicht auf einer Geraden liegen, sondern auf einer Kurve.
Die grafische Darstellung der Größenpaare einer indirekten Proportionalität ergibt Punkte, die auf einer Hyperbel liegen. Über Hyperbeln werden wir im Hauptkurs noch Näheres erfahren. Momentan ist nur wichtig, zu wissen, dass produktgleiche Zahlenpaare im Gitternetz gezeichnet eine Hyperbel bilden. Die Proportionalitätskonstante, unsere feste Größe c, ist charakteristisch für den Verlauf dieser Kurve. Hierzu noch ein Beispiel:
Wie viele Tiere kann der Bauer noch kaufen? Wie wir hörten, fressen 20 Kühe 150 Tage an dem Futtervorrat. Wir können das als kleine Gleichung darstellen mit 20 Kühen mal 150 Tage gibt den zur Verfügung stehenden Futtervorrat. Auf der linken Seite der Gleichung steht ein Produkt aus den Größen Kühe-Anzahl und Tage-Anzahl.
Es ist nun egal, wie wir die einzelnen Faktoren dieses Produktes belegen, es muss nur stets gewährleistet sein, dass der Produktwert immer dem vorhandenen Futtervorrat entspricht. Das bedeutet, wenn weniger Kühe fressen, reicht der Vorrat länger. Und umgekehrt ist der Vorrat schneller aufgebraucht, wenn mehr Kühe daran fressen.
Ein typisches Beispiel für eine indirekte Proportionalität.
Der Viehhändler stellte im Film fest, dass man nur noch von 120 Wintertagen ausgehen muss. Die Anzahl der Tage verringert sich, demnach könnte man die Anzahl der Tiere erhöhen.
Schauen wir uns die neue Situation einmal an.
Eine nicht bekannte Anzahl von Kühen soll 120 Tage von dem Futtervorrat fressen; somit haben wir ein Gleichungssystem. Stimmen die rechten Seiten überein, so müssen auch die linken Seiten übereinstimmen.
Anstelle des Fragezeichens könnten Sie sich auch einen Platzhalter x denken. Sie erkennen, dass ein Zahlenwert für die Größe des Futtervorrats nicht erforderlich ist, da bei einer indirekten Proportionalität die produktgleichen Zahlenpaare miteinander verglichen werden. Und das gibt dann eine Gleichung, die nach einer Variablen, sprich einem Platzhalter, aufgelöst werden muss; in unserem Beispiel nach der Anzahl der Kühe. Dazu teilen wir unsere Gleichung durch 120 Tage und erhalten die gesuchte Anzahl von Kühen (über den Term 20 Kühe mal 150 Tage geteilt durch 120 Tage ) mit 25 Kühen. Unser Bauer kann sich also fünf Kühe mehr in den Stall stellen und somit die Rendite aus dem Milchverkauf steigern.