GRIPS Mathe 1 Negative Zehnerpotenzen

Die Planetenentfernungen werden mit riesigen Zahlen dargestellt. Es gibt aber auch ganz winzige Zahlen. Dazu macht Sebastian Wohlrab einen Versuch mit einem Granitblock im Deutschen Museum. Wenn man sich auf diesen Granitblock stellt, zeigt das Messgerät an, wie weit sich der Granitblock durchbiegt.
Melanie und Sadik stellen sich auf den Block und sind überrascht. Das Messgerät zeigt tatsächlich eine Zahl an: 0,000000749 m. Diese unglaublich kleine Zahl kannst du kürzer mit einer negativen Zehnerpotenz darstellen.
Zehnerpotenzen bei kleinen Zahlen

Ähnlich wie große Zahlen kannst du auch kleine Zahlen als Zehnerpotenzen darstellen. Der Exponent (die Hochzahl) wird dabei negativ.
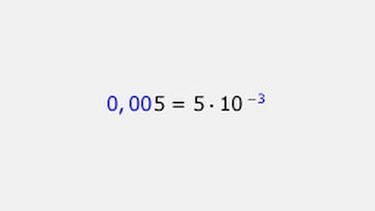
Als negative Zehnerpotenz sieht das Ganze dann so aus.

Der Granitblock hat sich um 0,000000749 durchgebogen. Auch diese Zahl kannst du als Zehnerpotenz darstellen.
Die Grafik zeigt dir eine mögliche Darstellungsart.
In folgender Tabelle findest du weitere Beispiele für negative Zehnerpotenzen:
| Zahl | Zerlegung | Zahl als Zehnerpotenz |
|---|---|---|
| 0,005 | 5 · 0,001 | 5 · 10-3 |
| 0,00007 | 7 · 0,00001 | 7 · 10-5 |
| 0,0057 | 5,7 · 0,001 | 5,7 · 10-3 |
| 0,00000125 | 1,25 · 0,000001 | 1,25 · 10-6 |
Negative Zehnerpotenz

Der negative Exponent der Zehnerpotenz gibt an, um wie viele Stellen du das Komma nach links verschieben musst, wenn du die Zahl ausschreiben willst. Nicht belegte Stellen füllst du mit Nullen auf.
