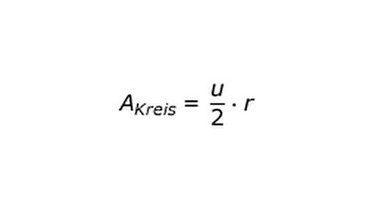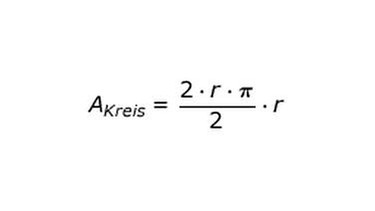GRIPS Mathe 20 Kreisfläche
Wer viel arbeitet, soll auch gut essen. Sebastian Wohlrab, Niklas und Charlotte haben sich eine Pizza verdient. Doch was ist günstiger: eine Jumbopizza oder zwei normale Pizzas? Dieses Rätsel lässt sich ganz leicht mit der Flächenformel für den Kreis lösen.
Auf dieser Seite geht es um den Flächeninhalt von Kreisen. Zunächst lernst du, mit welcher Formel du den Flächeninhalt eines Kreises berechnest. Anschließend erfährst du die Antwort darauf, welche Pizzavariante denn nun günstiger ist.
Der Flächeninhalt eines Kreises
Vor der Pizzabestellung überlegen Seabstian Wohlrab, Niklas und Charlotte welche Pizza größer ist. Eine Jumbopizza mit einem Durchmesser von 50 cm oder zwei normale Pizzas mit einem Durchmesser von 32 cm?
Um die Frage beantworten zu können, müssen die Flächeninhalte der Pizzas berechnet werden.
Mit Hilfe der Rechtecksformel kannst du die Formel für den Kreis finden.
Den Flächeninhalt eines Rechtecks berechnest du, indem du die Länge (a) mit der Breite (b) multiplizierst:
ARechteck = a · b
Jetzt zeigen wir dir, wie du zur Kreisformel kommst. Mach mit!
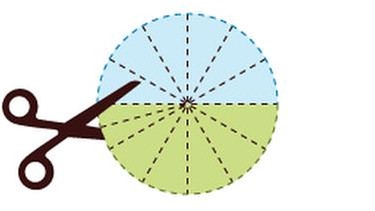
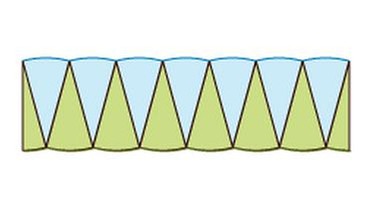
1. Kreis als "Rechteck"
1. Kreis zeichnen
Teile einen Kreis in 12 gleich große Teile.
Markiere 6 davon in einer Farbe und die anderen 6 in einer anderen Farbe.
Sieh dir dazu die Abbildung an.
2. Formel finden
1. Schritt
Kreiselemente der Rechteckformel zuweisen
Du hast gesehen, dass man einen Kreis auch als Rechteck darstellen kann.
Deshalb kannst du im nächsten Schritt die Flächenformel für das Rechteck anwenden: A = a · b
a. Die Länge der Seite a des Rechtecks entspricht dem halben Umfang u des Kreises.
b. Die Länge der Seite b entspricht dem Radius r.
Du hast die Formel kennengelernt, mit der du die Kreisfläche berechnen kannst. Diese Formel solltest du dir gut merken!
Formel Kreisfläche
Mit dieser Formel berechnest du die Kreisfläche.
Der Flächeninhalt der Pizza
Zurück zur Pizza. Du kennst jetzt die Formel, mit der du den Flächeninhalt eines Kreises ausrechnen kannst.
Welche Pizza ist nun größer: die Jumbopizza mit einem Durchmesser von 50 cm oder zwei normale Pizzas mit einem Durchmesser von 32 cm?
Kreisfläche berechnen
Pizza 32 cm
Pizza mit Durchmesser 32 cm
Gegeben: Durchmesser d = 32 cm, Der Radius r ist die Hälfte des Durchmessers, also 16 cm.
Gesucht: Flächeninhalt A der Pizza
In der Grafik siehst du, wie du den Flächeninhalt der Pizza berechnest.
Ergebnis: Der Flächeinhalt dieser Pizza beträgt 803,84 cm².
Der Radius eines Kreises
Wenn du den Flächeninhalt eines Kreises kennst, kannst du auch seinen Radius berechnen. Hier ein Beispiel:
Radius berechnen
Gegeben: Kreisfläche = 2826 cm²
Gesucht: Radius r
In der Grafik kannst du sehen, wie du den Radius r des Kreises berechnest. Dazu musst du die Formel so umstellen, dass r auf einer Seite steht.
Ergebnis: Der Radius des Kreises beträgt 30 cm.