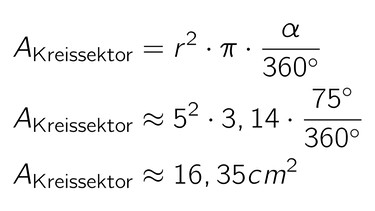GRIPS Mathe 20 Kreissektoren
Nicht nur der Flächeninhalt einer ganzen Pizza lässt sich berechnen, auch den Flächeninhalt eines einzelnen Pizzastücks kannst du herausfinden. Wie das geht erfährst du hier. Ein Stück eines Kreises, das aussieht wie ein Pizzastück heißt übrigens "Kreissektor".
Kreissektor
Ein Kreissektor ist ein Teil einer Kreisfläche, der von einem Stück des Umfangs und zwei Linien zum Mittelpunkt (zwei Radien) begrenzt wird.
Tipp: Denke bei einem Kreissektor einfach an ein Stück Kuchen oder Pizza.
Flächeninhalt Kreissektor
Sebastian Wohlrab, Niklas und Charlotte wollen ihre Pizza in 5 gleich große Stücke aufteilen.
Wie groß ist dann eigentlich jedes einzelne Stück?
1. Berechnung durch "einfaches Teilen"
Da die Pizza in fünf gleich große Stücke aufgeteilt werden soll, gibt es einen ganz einfachen Weg, den Flächeninhalt (die "Größe") eines Pizzastücks zu berechnen:
Rechenweg durch "Teilen"
1. Schritt: Kreisfläche berechnen
Zunächst wird der Flächeninhalt des ganzen Kreises berechnet.
2. Schritt: Kreisfläche aufteilen
Die Pizza soll nun in fünf gleichgroße Stücke (Kreissektoren) aufgeteilt werden.
Das geht ganz einfach: Du teilst die Gesamtfläche durch die Anzahl der Pizzastücke:
1962,50 cm² : 5 = 392,50 cm²
Lösung
Antwort: Ein Pizzastück hat einen Flächeninhalt von 392,50 cm².
2. Berechnung mit der Formel
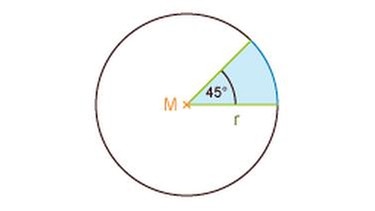
Wenn die Kreissektoren ("Pizzastücke") unterschiedlich groß sind, dann kannst du nicht einfach die Kreisfläche durch die Anzahl der Kreissektoren teilen. Dann brauchst du die Formel.
Den Flächeninhalt einer ganzen Pizza berechnest du mit der Kreisformel:
AKreis = r² · π
Möchtest du nun aber wissen, wie groß der Flächeninhalt eines einzelnen Pizzastücks ist, dann brauchst du zusätzlich noch eine Winkelangabe.
Der Vollwinkel ("einmal rundum") eines Kreises beträgt 360°.
Der Winkel des einzelnen Kreissektors ("Pizzastück") hat dann nur die Größe eines Teiles von 360°, hier zum Beispiel 72°.
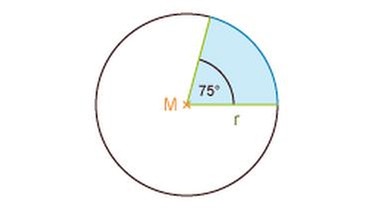
Formel Kreissektor
Mit dieser Formel berechnest du den Flächeninhalt eines Kreissektors.
Für α setzt du die Größe des Winkels des Kreissektors ein.
Beispiel: Hat der Kreissektor einen Winkel von 50°, dann ist α = 50°.
So berechnest du den Flächeninhalt eines Pizzastücks mit der Formel:
Rechenweg mit der Formel
1. Schritt: Vollwinkel
Ein Kreis hat einen Winkel von 360°.
2. Schritt: Mittelpunktswinkel
Die Pizza wird in fünf gleich große Stücke aufgeteilt. Der Winkel eines der Stücke ist dann natürlich nur einen Bruchteil von 360° groß.
Bei 5 Teilen ist der Mittelpunktswinkel 360° : 5 = 72° groß.
3. Schritt: Kreissektor
Jetzt kannst du die Fläche eines Kreissektors (eines Pizzastücks) berechnen.
Dazu setzt du die Werte in die Kreissektor-Formel ein.
Lösung
Wenn eine Pizza in 5 gleich große Teile geteilt wird, dann hat jedes einzelne Stück einen Winkel von 72° und besitzt einen Flächeninhalt von 392,50 cm².
Antwort: Ein Stück der Pizza ist 392,50 cm² groß.
Übungsaufgaben
Jetzt bist du an der Reihe. Hier kannst du testen, ob du verstanden hast, wie du den Flächeninhalt eines Kreissektors berechnest.
Berechne den Flächeninhalt des Kreissektors
Aufgabe 1
Gegeben: Radius r = 5 cm, Mittelpunktswinkel α = 75°
Gesucht: Fläche A des Kreissektors
Lösung
Lösung zu Beispiel 1
Aufgabe 2
Gegeben: Radius r = 8 cm, Mittelpunktswinkel α = 45°
Gesucht: Fläche A des Kreissektors
Lösung
Lösung zu Beispiel 2