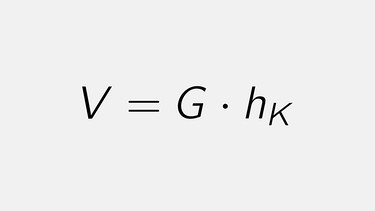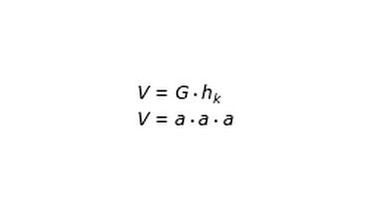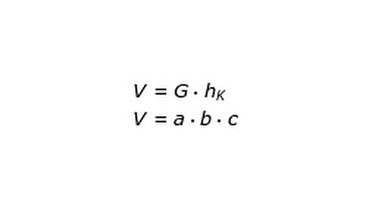GRIPS Mathe 22 Wie berechnet man das Volumen von Prismen?
Für alle Prismen gibt es eine allgemeine Formel zur Berechnung ihres Rauminhalts (Volumens).
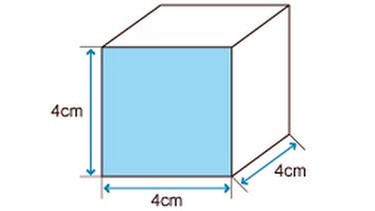
Volumen Prisma
Diese allgemeine Formel solltest du dir merken:
Volumen = Grundfläche · Höhe des Körpers
V = G · hK
Die allgemeine Formel kannst du leicht an das jeweilige Prisma anpassen und so das Volumen verschiedener Prismen berechnen.
Wichtig sind dabei drei Schritte:
1. Schritt: Beachte immer zuerst die allgemeine Grundformel: V = G · hk
2. Schritt: Berechne dann die Grundfläche des Prismas.
3. Schritt: Multipliziere das Ergebnis mit der Höhe des Prismas.
Beispiele zur Volumenberechnung
Volumen: Würfel
Würfel
Dieser Würfel hat eine Seitenlänge von 4 cm.
Wie groß ist sein Volumen?
Volumen: Quader
Quader
Gegeben ist ein Quader mit diesen Maßen.
Wie groß ist sein Volumen?
Volumen: Dreiecksprisma (Dreieckssäule)
Dreiecksprisma
Gegeben ist ein Dreiecksprisma mit diesen Maßen.
Wie groß ist sein Volumen?
