GRIPS Mathe 25 Achsensymmetrie
Überall auf der Welt begegnen dir symmetrische Darstellungen. Sei es in der Tier- und Pflanzenwelt oder in der Architektur. Auch dein Gesicht ist weitgehend symmetrisch. Doch was bedeutet Symmetrie genau? Und welche Arten von Symmetrie gibt es? Das erfährst du auf den folgenden Seiten.

Ob Tiger, Kleeblatt oder Kirche – alle haben eines gemeinsam: sie sind symmetrisch.
Schau dir die folgenden Beispiele einmal genau an. Was fällt dir auf, wenn du die linke und rechte Seite dieser Tiere, Pflanzen, Gebäude und Gegenstände betrachtest?
Symmetrische Erscheinungen
Alle Beispiele oben haben eines gemeinsam: Sie besitzen eine Symmetrieachse. Was eine Symmetriachse ist, siehst du an diesem Schmetterling:

Falte die beiden Flügelhäften des Schmetterlings an der orangenen Linie. Was stellst du fest?
Beide Flügelhälften passen genau aufeinander. Sie sind deckungsgleich.
Achsensymmetrie
- Wenn man eine Figur so falten kann, dass beide Hälften genau aufeinander passen, nennt man sie achsensymmetrisch.
- Die Faltlinie wird als Symmetrieachse oder auch als Spiegelachse bezeichnet.
- Die beiden Hälften sind deckungsgleich.
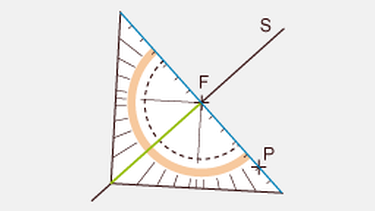
Achsenspiegelung eines Punktes
In der Abbildung siehst du, wie du zu einem Punkt P seinen gespiegelten Bildpunkt P' zeichnen kannst:
Achsenspiegelung eines Punktes
- Die Bildpunkte (= gespiegelte Punkte) werden mit A', B', C'... bezeichnet
- Die Verbindungslinie von Urpunkt und Bildpunkt steht senkrecht auf der Symmetrieachse.
- Jeder Bildpunkt hat von der Symmetrieachse den gleichen Abstand wie der entsprechende Urpunkt.
- Das heißt, die senkrechte Verbindungslinie zwischen den beiden Punkten wird von der Symmetrieachse halbiert.
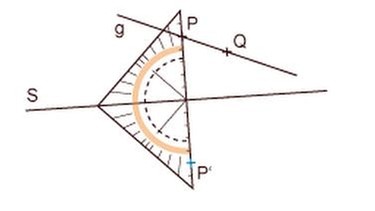
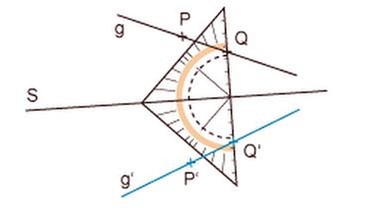
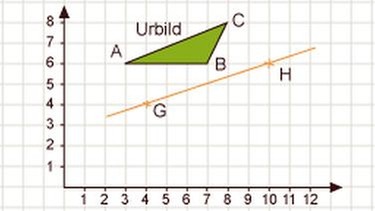
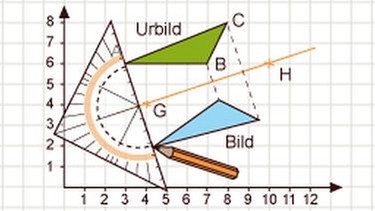
Achsenspiegelung einer Geraden
Genauso wie du einen Punkt spiegeln kannst, kannst du auch eine Gerade spiegeln. Wie das geht, siehst du an folgendem Beispiel:
Achsenspiegelung einer Geraden
Zeichnen achsensymmetrischer Figuren
Das Spiegeln von geometrischen Figuren stellt für dich jetzt sicher kein Problem mehr da: