GRIPS Mathe 25 Drehsymmetrie
Auch bei der Drehsymmetrie geht es um Spiegelbilder von geometrischen Figuren.
Sieh dir mal diese Bilder an, was fällt dir dabei auf?
Drehsymmetrische Erscheinungen
Schneeflocke
Schneeflocken sind drehsymmetrisch. Wenn du sie um ihren Mittelpunkt drehst, wirst du feststellen, dass ihre "Zacken" deckungsgleich sind.
Eine Figur ist drehsymmetrisch, wenn sie bei Drehung um weniger als 360° wieder auf sich selbst abgebildet wird.
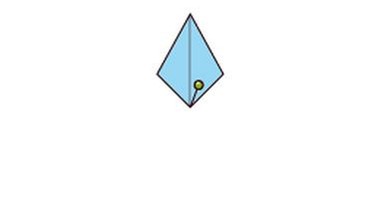
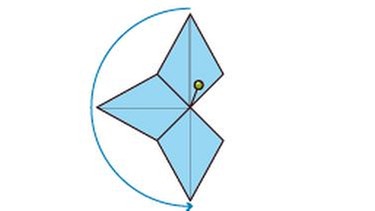
Drehung eines Drachenvierecks
Ein Drachenviereck wird drei Mal um 90° um einen an der Figur liegenden Drehpunkt gedreht. Die Drehung erfolgt gegen den Uhrzeigersinn:
Drehung eines Drachenvierecks
Ausgangsfigur
Ausgangsfigur Drachenviereck
Der Drehpunkt einer Figur kann an verschiedenen Stellen liegen:
- an der Figur (Beispiel: siehe Drachenviereck oben)
- in der Figur (Beispiele: siehe Steuerrad und Verkehrszeichen Kreisverkehr)
- außerhalb der Figur (Beispiel: siehe Drehung des Dreiecks unten)
Beispiel für einen Drehpunkt außerhalb der Figur
Gegeben ist das Dreieck ABC, das um einen Drehpunkt Z um 90° gepspiegelt werden soll:
Hier wurde das Dreieck ABC um einen Drehpunkt Z um 90° im Uhrzeigersinn gedreht. Das Bilddreieck A'B'C' ist genau deckungsgleich zum Urdreieck.
Drehsymmetrie
Um eine ganz bestimmte Drehung ausführen zu können, brauchst du genau drei Angaben:
- Die Lage des Drehpunktes, um den gedreht wird.
- Die Drehrichtung, die angibt, ob es eine Drehung im Uhrzeigersinn oder eine Drehung gegen den Uhrzeigersinn ist.
- Den Drehwinkel, der dir sagt, wie weit du drehen musst.
Figuren, die man durch drehen auf sich selbst abbilden kann, heißen drehsymmetrisch.
Jeder Punkt wird dabei durch Drehung um den Drehpunkt mit dem Drehwinkel auf seinen Bildpunkt abgebildet.