GRIPS Mathe 28 Zeichnen von regelmäßigen Vielecken

Kennzeichen regelmäßiger Vielecke
Regelmäßige Vielecke besitzen bestimmte Eigenschaften mit deren Hilfe du sie zeichnen kannst:
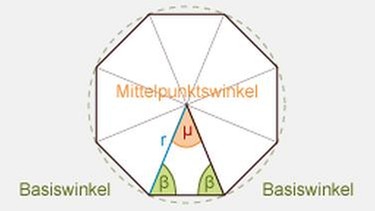
- Alle Seiten sind gleich lang.
- Alle Ecken liegen auf einer Kreislinie (Umkreis).
- Jedes regelmäßige Vieleck setzt sich aus so vielen gleichen Dreiecken (Bestimmungsdreiecke) zusammen, wie es Ecken (Seiten) hat.
- Die Basiswinkel dieser Bestimmungsdreiecke sind immer gleich groß.
- Alle Mittelpunktswinkel sind gleich groß.
Notwendige Berechnungen
Ein regelmäßiges Vieleck zu zeichnen, ist gar nicht so schwer. Dazu musst du allerdings zuerst den Mittelpunktswinkel und die Basiswinkel berechnen. Das geht so:
Winkelberechnungen
Berechnung des Mittelpunktswinkels
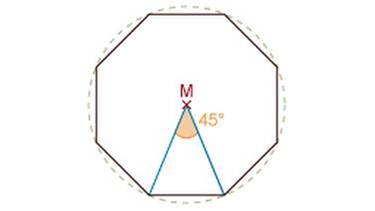
Den Mittelpunktswinkel erhältst du, wenn du 360° (Vollkreis) durch die Anzahl der Ecken teilst.
Beispiel: Der Mittelpunktswinkel bei einem regelmäßigen Achteck beträgt demnach 360°: 8 = 45°.
Berechnung der Bassiswinkel
Möchtest du die Basiswinkel des Bestimmungsdreiecks berechnen, gehst du bei unserem Beispiel (Achteck) so vor:
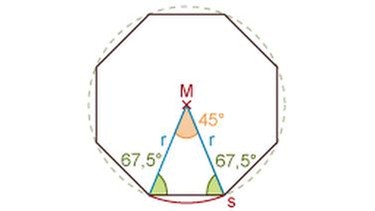
Die Winkelsumme im Dreieck beträgt immer 180°. Da beide Basiswinkel gleich groß sind, musst du nur den Mittelpunktwinkel von 180° abziehen und das Ergebnis durch 2 teilen:
Basiswinkel =
(180 ° - Mittelpunktswinkel) : 2
Beispiel: Der Mittelpunktswinkel beträgt 45°. Ein Basiswinkel ist demnach
(180° - 45°) : 2 = 67,5° groß.
Aufgabentypen
In der Geometrie gibt es verschiedene Aufgabenstellungen zum Vieleck. Wir zeigen dir zwei davon und du erfährst, wie du schrittweise ein regelmäßiges Neuneck zeichnest.
Aufgabe 1: Radius gegeben
Zeichne ein regelmäßiges Neuneck mit dem Umkreisradius 5 cm.
So gehst du vor:
Aufgabe 2: Seite gegeben
Zeichne ein regelmäßiges Neuneck mit der Seitenlänge 3 cm.
So gehst du vor:
Hinweis: Seitenlänge s
Manchmal ist nur der Umfang eines regelmäßigen Vielecks gegeben, zum Beispiel: Umfang 6-Eck = 30 cm. Um eine Seite auszurechnen, musst du den Umfang erst durch die entsprechende Anzahl der Ecken teilen, um die Länge einer Seite zu erhalten. Hier: s = 30 cm : 6 = 5 cm.