GRIPS Mathe 32 Beispiel für eine proportionale Zuordnung

Aufgabe: Flyer verteilen

Im Film möchte Felix 800 Flyer verteilen. In einer Stunde schafft er ungefähr 90 Stück.
Wie viel Zeit muss er einplanen?
Grafische Lösung der Aufgabe
Da es sich hier um eine proportionale Zuordnung handelt, gilt:
- Je mehr Flyer zu verteilen sind, desto länger braucht Felix.
- Da Felix 90 Flyer in 1 Stunde schafft, braucht er für 180 Flyer doppelt so lang, nämlich 2 Stunden. Für die dreifache Anzahl an Flyern (270 Stück) braucht er dreimal so lang (3 Stunden) usw.
Diese Zuordnung kann in einem Koordinatensystem dargestellt werden. Grundlage dafür ist eine Wertetabelle:
| Anzahl der Flyer (Stück) | 90 | 180 | 270 | 360 | 450 | 540 |
|---|---|---|---|---|---|---|
| Zeit in Stunden (h) | 1 | 2 | 3 | 4 | 5 | 6 |
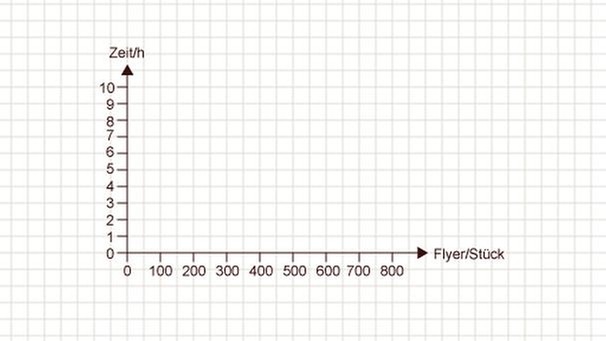
Jetzt kannst du das Koordinatensystem zeichnen:
Merkmale des Graphen
- Der Graph dieser proportionalen Zuordnung ist eine Linie, genauer gesagt eine Halbgerade. Eine solche Zuordnung wird auch als lineare Funktion bezeichnet.
- Der Graph einer linearen Funktion geht durch den Nullpunkt.
- Um den Graphen zeichnen zu können, genügt dir ein einziges Wertepaar aus der Tabelle. Denn eine Gerade wird durch zwei Punkte bestimmt und der Nullpunkt liegt bereits fest.
Rechnerische Lösung der Aufgabe
Wie lange Felix genau für seine 800 Flyer braucht, kannst du mit dem Dreisatz in drei Schritten berechnen:

1. Zeile: In die erste Zeile schreibst du, was du schon weißt: Felix schafft in 1 Stunde 90 Flyer.
2. Zeile: Auf der Seite, auf der du das Endergebnis kennst
(800 Flyer), musst du auf die Einheit (1 Flyer) kommen, indem du durch 90 teilst. Wichtig: Vergiss nicht beide Seiten durch 90 zu teilen!
3. Zeile: Um die Zeit für 800 Flyer zu berechnen, musst du nun nur noch beide Seiten mit 800 multiplizieren.
Antwort: Felix braucht für 800 Flyer rund 9 Stunden.