GRIPS Mathe Beispiel für eine umgekehrt proportionale Zuordnung

Wir übertragen die neuen Erkenntnisse auf unser Flyer-Beispiel:
Aufgabe: Flyer verteilen

Nach knapp zwei Stunden sind nur 170 von 800 Flyern verteilt. Felix wird klar, dass dieser Auftrag an einem Nachmittag alleine nicht zu schaffen ist. Er braucht dringend Hilfe von seinen Freunden.
Zur Erinnerung: Eine Person schafft in einer Stunde (= 60 Minuten) 90 Flyer.
Wie viele Personen sind nötig, wenn die restlichen 630 Flyer in den verbleibenden zwei Stunden verteilt werden sollen?
1. Wie lange braucht 1 Person für 630 Flyer?

Mit dem Dreisatz kannst du berechnen, wie lange eine Person für 630 Flyer brauchen würde.
Ergebnis: Eine Person wäre 420 Minuten (= 7 Stunden) beschäftigt.
2. Lösung mit Hilfe der Wertetabelle
Mit Hilfe der Information aus Schritt 1 kannst du eine Wertetabelle erstellen.

Denke daran: Bei einer umgekehrt proportionalen Funktion gilt:
je mehr - desto weniger. Das heißt, 2 Personen können die Flyer in der Hälfte der Zeit austeilen, 3 Personen erledigen die Aufgabe in einem Drittel der Zeit usw.
| Personen | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Zeit / Minuten | 420 | 210 | 140 | 105 | 84 | 70 | 60 | 52,5 |
Da nur noch 2 Stunden (= 120 Minuten) zur Verfügung stehen, braucht Felix Hilfe von mindestens 3 Freunden. Denn zu viert schaffen sie es in 105 Minuten.
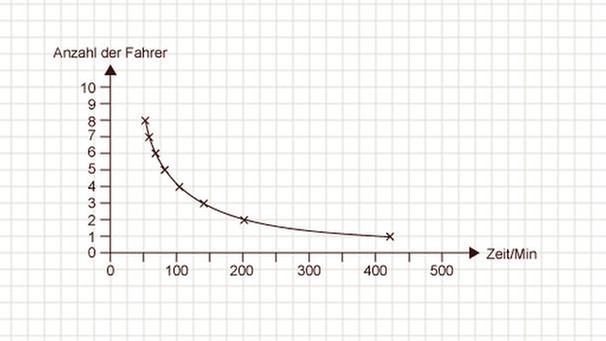
3. Graphische Lösung
Du kannst die Anzahl der benötigten Personen auch graphisch herausfinden:
Antwort: Um alle Flyer in 120 Minuten zu verteilen, sind 4 Personen nötig.