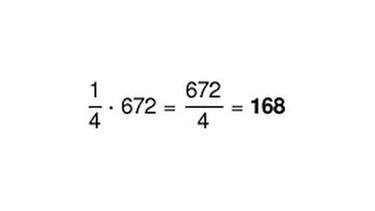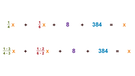
Auf der vorherigen Seite haben wir die Gleichung für die verschiedenen Gruppen von Autofahrern aufgestellt, die zu schnell gefahren sind. Jetzt wird diese Gleichung in mehreren Schritten gelöst.

1. Hauptnenner festlegen

Wenn du dir die Brüche in der Gleichung ansiehst, stellst du fest, dass sie unterschiedliche Nenner haben: 4 und 6. Aus der Bruchrechnung weißt du, dass man zwei Brüche mit unterschiedlichem Nenner nicht einfach addieren darf. Du musst die Brüche erst gleichnamig machen, das heißt einen gemeinsamen Nenner suchen, bevor du weiterrechnen kannst.

So suchst du das kleinste gemeinsame Vielfache von 1/4 und 1/6:

Vielfache von 4: 4, 8, 12, 16, 20 ...
Vielfache von 6: 6, 12, 18 ...

Die erste gemeinsame Zahl der Vielfachen von 4 und 6 ist 12. Damit steht der Hauptnenner fest und die beiden Brüche können auf den Hauptnenner 12 erweitert werden:

2. Mit dem Hauptnenner multiplizieren

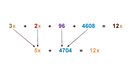
Mit einem Trick kannst du die Brüche verschwinden lassen. Dazu multiplizierst du die komplette Gleichung, das heißt jeden einzelnen Term auf beiden Seiten der Gleichung, mit dem Hauptnenner. Danach kannst du die Gleichung wie gewohnt lösen:

3. Anzahl der zu schnell gefahrenen Fahrzeuge ermitteln

Damit sind wir aber noch nicht fertig. Gesucht ist die Anzahl der zu schnell gefahrenen Fahrzeuge pro Geschwindigkeitsgruppe:

Oben haben wir berechnet, dass von insgesamt 672 Fahrzeugen (x = 672) die Geschwindikeit gemessen wird. Wenn du die Gesamtzahl der Fahrzeuge weißt, kannst du die Anzahl der Fahrzeuge der einzelnen Geschwindigkeitsgruppen bestimmen. Dazu ersetzt du im jeweiligen Term die Variable x durch die Lösung der Gleichung (672) und berechnest den Term:

Damit kannst du die Ausgangsfrage "Wie viele Fahrzeuge sind insgesamt zu schnell?" beantworten:

Antwort: Insgesamt sind 288 der 672 überprüften Fahrzeuge zu schnell unterwegs.