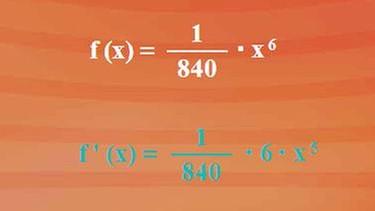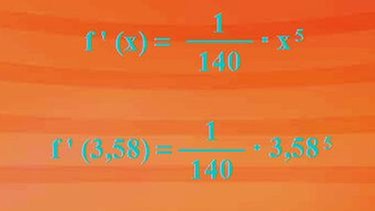Ableitungsfunktion in Anwendungen Beispiel zur Grundableitungsregel
An einem praktischen Beispiel wenden wir jetzt die Grundableitungsregel an. Dazu begeben wir uns auf eine Skaterbahn, die - mathematisch betrachtet - einer weit auseinandergezogenen Parabel entspricht.
Wir wollen nun die in der letzten Lektion erarbeitete Grundableitungsregel an einem Beispiel anwenden.
Die Skaterbahn - eine Parabel
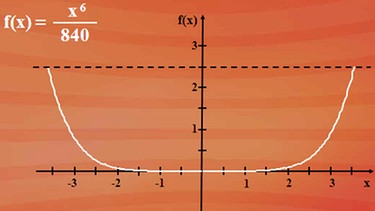
Die Skaterbahn ähnelt einer weit auseinandergezogenen Parabel.
Die Skaterbahn ähnelt einer weit auseinandergezogenen Parabel. Der genaue Kurvenverlauf entspricht einer Funktion sechsten Grades mit nebenstehender Funktionsgleichung. Bei Klick auf die Abbildung sehen Sie die dazugehörige Funktionskurve. Sie entspricht einem Längsschnitt der Skaterbahn. Wir können jetzt für jeden Punkt der Skaterbahn die Steigung angeben, da wir wissen, dass die Ableitung der Grundfunktion die Steigung für jeden beliebigen Punkt mit der x-Koordinate x0 angibt. Trotzdem ist es nicht ganz so einfach:
Die Bahnhöhe ist bekannt, doch wie lang ist die Bahn? Klicken Sie bitte auf die Lupe.
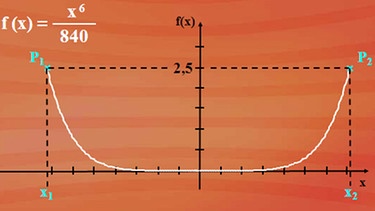
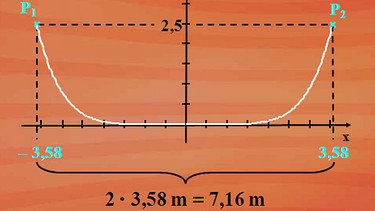
Wir wissen, dass die Bahn eine Höhe von 2,50 Meter hat. Es ist uns aber nicht bekannt, welche Länge die Bahn einnimmt. Sie besitzt aber eine Symmetrieachse. Der Verlauf der Bahn ist durch die Funktionsgleichung bekannt. Somit ist es uns möglich, zu berechnen, bei welchem x-Wert der Graph der Funktion den f(x)-Wert 2,5 hat. Der Funktionswert entspricht der Höhe der Bahn. Wie können wir das berechnen?
Für f(x) = 2,5 gibt es zwei Punkte auf dem Graphen.
Für f(x) = 2,5 gibt es zwei Punkte auf dem Graphen. Einen Punkt P1 mit der Abszisse x1 und einen Punkt P2 mit der Abszisse x2. Die Abszissen der Punkte P1 und P2 werden wir jetzt bestimmen, wobei deren Ordinate 2,5 ist.
Abszisse und Ordinate
Abszisse ist der Begriff für die x-Koordinate eines Punktes. Der f(x)-Wert heißt Ordinate des Punktes. Jeder Punkt in einer Ebene besitzt also eine Abszisse x und eine Ordinate f(x).
Bestimmung der Abszissen
Berechnung der beiden x-Werte - klicken Sie bitte auf die Lupe.
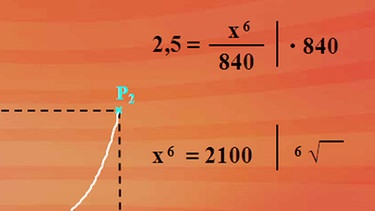
Um die Abszissen der Punkte P1 und P2 zu bestimmen, setzen wir in der Funktionsgleichung für f(x) den Wert 2,5 ein. Wir erhalten nebenstehende Bestimmungsgleichung. Die Gleichung mit 840 multipliziert, führt zur umgeformten Gleichung x6 = 2100. Um x zu erhalten, radizieren wir mit dem Wurzelexponenten 6. x1 und x2 ist dann plus oder minus sechste Wurzel aus 2100.
In der weiteren Berechnung erhalten wir die x-Werte und wissen nun, wie lang die Bahn ist. Klicken Sie bitte auf die Lupe.
Wir wählen als Lösung x1 minus sechste Wurzel aus 2100 gleich minus 3,58 und für x2 erhalten wir somit plus 3,58.
Jetzt kennen wir nach der Höhe auch die Länge der Skaterbahnkonstruktion. Sie beträgt 7,16 Meter - klicken Sie bitte auf nebenstehende Abbildung.
Ermittlung der Steigung
Ermittlung der Steigung - klicken Sie bitte auf die Lupe.
Um die Steigung am Beginn der Bahn ermitteln zu können, müssen wir in die Ableitung der Funktionsgleichung den x0-Wert 3,58 einsetzen. Er entspricht der Abszisse des Punktes P2. Die erste Aufgabe ist jetzt, die Ableitung der Funktion f(x) = x6 / 840 zu bestimmen. Dazu benötigen wir die Grundableitungsregel aus der letzten Lektion. Erinnern Sie sich noch: Hochzahl nach vorne und um eins vermindert - siehe nebenstehende Abbildung.
Ermittlung der Steigung - klicken Sie bitte auf die Lupe.
Jetzt ermitteln wir die Steigung im Punkt mit der x-Koordinate 3,58. Die Ableitung bei x0 = 3,58 ist also gefragt. Wie in nebenstehender Berechnung gezeigt, erhalten wir als Ergebnis: Die Steigung des Graphen im Punkt P2 beträgt 4,2. Dieses Ergebnis können wir am Graphen der Ableitungsfunktion nachprüfen.
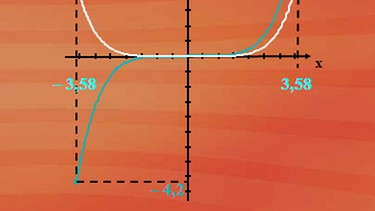
Prüfung am Graphen der Ableitungsfunktion
Der Graph von f'(x) = 1/140 mal x5 hat bei x gleich 3,58 wirklich den f(x)-Wert 4,2.
Prüfung am Graphen der Ableitungsfunktion - klicken Sie bitte auf die Lupe.
An unserer Skaterbahnkurve kann man schön erkennen, dass für jeden x-Wert der Skaterbahnkurve aus dem Graphen der Ableitungsfunktion direkt die dazugehörige Steigung abgelesen werden kann. Bei minus 3,58 zum Beispiel ist die Steigung m = -4,2.