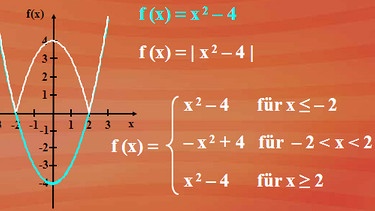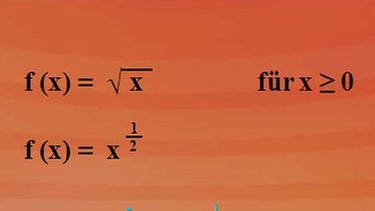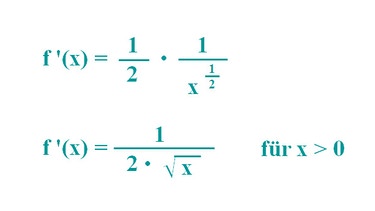Ganzrationale Funktionen, wie wir sie bisher betrachtet haben, stellen nur einen kleinen Teil der tatsächlich auftretenden Funktionen dar. Praktische Probleme werden meist über empirische Funktionen beschrieben. Das sind Funktionen, die nicht über eine Rechenvorschrift bestimmt werden, sondern über Werte aus Messungen festgelegt sind. Eine empirische Funktion könnte also bei einer Verkehrszählung entstehen. Es ist der funktionale Zusammenhang zwischen der Anzahl der vorbeigefahrenen Fahrzeuge und der Zeit. Oftmals lassen sich diese Funktionen nur näherungsweise differenzieren. Eine Betragsfunktion ist das einfachste Beispiel einer Funktion, die nicht an allen Stellen eine eindeutige Tangente besitzt:

Betragsfunktionen

Ableitungsfunktion in Anwendungen - klicken Sie bitte auf die Lupe.

Nehmen wir die Funktion f(x) = Betrag von x² minus 4. Der Parabelbogen für x² minus 4 ist nicht schwer zu zeichnen - entweder über eine Wertetabelle oder über das Auszählen vom Scheitelpunkt S ausgehend. Betrag bedeutet, dass nur positive Funktionswerte entstehen können. Der Bogen unterhalb der x-Achse wird nach oben gespiegelt. Die Betragsfunktion lässt sich aufgegliedert anschreiben als:

Rechtsseitige und linksseitige Annäherung

linksseitige und rechtsseitige Annäherung, Sekantensteigung und Tangentensteigung - klicken Sie bitte auf die Lupe.

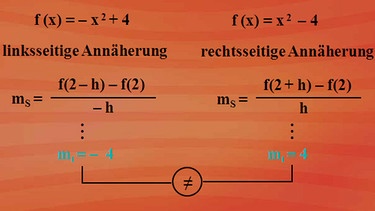
Wir werden nun an der Stelle x = 2 eine rechtsseitige und eine linksseitige Annäherung mit dem uns bekannten kleinsten Abstand h durchführen. Dafür werden wir nochmals eine Sekantensteigung und die daraus resultierende grenzwertige Tangentensteigung ermitteln. Für die linksseitige Annäherung an x = 2 gilt f(x) = minus x² plus 4. Für die rechtsseitige Annäherung gilt f(x) = x² minus 4. Die Sekantensteigung ms in Abhängigkeit von h sehen Sie nebenstehend. In die Funktion f(x) eingesetzt, erhalten wir die Tangentensteigung m_t = -4. Die rechtsseitige Annäherung führt zur Tangentensteigung 4: Klicken Sie auf nebenstehende Abbildung. Wir erhalten für ein und denselben Punkt unterschiedliche Tangentensteigungen.

Da keine eindeutig bestimmbare Tangentensteigung an der Stelle x = 2 bestimm_t werden kann, ist diese Betragsfunktion an der Stelle x₀ = 2 nicht differenzierbar. Soweit zu den Betragsfunktionen. Wie sieht es bei den Wurzelfunktionen aus?

Wurzelfunktionen

Nehmen wir die einfachste Wurzelfunktion, die Quadratwurzelfunktion f(x) = Wurzel aus x. Der Wert unter der Wurzel, der sogenannte Radikand, darf nicht kleiner als null sein.

Quadratwurzelfunktion - klicken Sie bitte auf die Lupe.

Über die Potenzschreibweise kann man statt Wurzel aus x auch x hoch ein halb schreiben. Jetzt haben wir eine Potenzschreibweise und können die Grundableitungsregel wieder anwenden – wie das funktioniert, sehen Sie bei Klick auf nebenstehende Abbildung.

Ableitungsfunktion in Anwendungen

Wir erhalten 1 durch 2 mal Wurzel aus x. Dieser Ableitungsterm ist nur für Werte größer als null definiert -  gleich null scheidet aus, weil man durch null nicht teilen darf. Somit steht fest, dass die Quadratwurzelfunktion an der Stelle x = 0 keine reelle Zahl als Grenzwert besitzt. Man kann wieder sagen, sie ist an der Stelle x₀ = 0 nicht differenzierbar. Das lässt sich auch grafisch erklären.

Grafische Darstellung der Quadratwurzelfunktion mit Tangente im Nullpunkt - klicken Sie bitte auf die Lupe.

Die Wurzelfunktion f’(x) = Quadratwurzel aus x ist die an der Winkelhalbierenden des ersten und dritten Quadranten gespiegelte quadratische Funktion f(x) = x². Die gezeichnete Wurzelfunktion hat deutlich sichtbar im Nullpunkt eine Tangente. Es ist die y-Achse, die senkrecht auf der x-Achse steht und somit die Steigung unendlich besitzt - was keine reelle Zahl ist. Jetzt ist also klar, dass die Wurzelfunktion f(x) = Quadratwurzel aus x nur für x größer als null differenzierbar ist. Die zugehörige Ableitungsfunktion bei x > 0 sehen Sie bei Klick auf nebenstehende Abbildung.

Wie wir gesehen haben, reicht die uns bekannte Grundableitungsregel aus, um alle Ableitungen von Funktionen herleiten zu können. Damit man nicht immer umständliche Herleitungen durchführen muss, stehen die wichtigsten Grundableitungen in der Formelsammlung.

Trigonometrische Funktionen

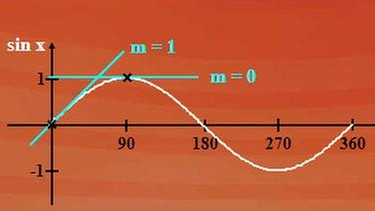
Grafische Darstellung der Funktion f(x) = sin x und ihrer Ableitung - klicken Sie bitte auf die Lupe.

Wir wollen nun noch zwei besondere Ableitungen herleiten: die Ableitungen der trigonometrischen Funktionen Sinus und Kosinus von x. Nebenstehend sehen Sie die Sinusfunktion und – bei Klick auf die Abbildung – die Steigung der Sinusfunktion. Im Punkt null ist die Steigung m = 1, bei 90 Grad ist die Steigung null und so weiter. Sicher komm_t Ihnen diese Kurve bekannt vor: Es ist die Kosinuskurve. Die Ableitung von Sinus x ist somit Kosinus x.

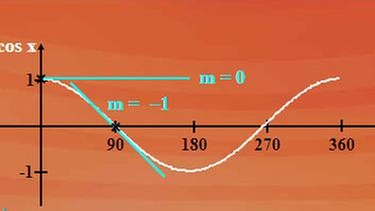
Grafische Darstellung der Funktion f(x) = cos x und ihrer Ableitung - klicken Sie bitte auf die Lupe.

Dasselbe Spiel noch mit der Kosinuskurve: Sie hat bei der Null die Steigung null, bei 90 Grad die Steigung -1. Bei 180 Grad die Steigung null, und so weiter. Es ist eine nach unten geklappte Sinuskurve. Die Funktion f(x) = cos x hat also die Ableitungsfunktion f’(x) = -sin x.