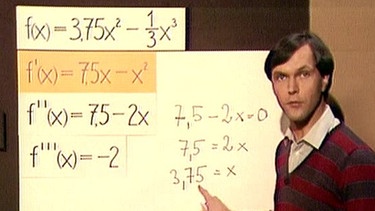Kurvendiskussion 2 Praktisches Beispiel
Nun wenden wir die erarbeiteten Regeln auf eine Beispielfunktion an.

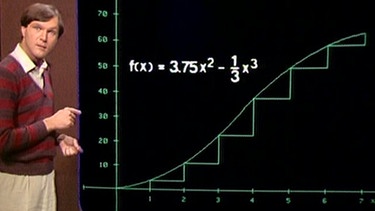
Betrachtet wird das Modell eines Bergs, auf den eine Seilbahn gebaut werden soll - siehe das Bild oben. Die Konstrukteure suchen nach der steilsten Stelle dieses Bergs.
Dazu wird das Modell auseinandergenommen, so dass nur noch der Querschnitt mit der Hangkurve zu sehen ist.
Die Hangkurve wird anschließend als Graph einer Funktion mit der Funktionsgleichung f’(x) = 3,75x2 – (1/3)x3 auf dem Computerbildschirm gezeigt. Um einen groben Überblick über den Verlauf der Steigung zu erhalten, werden Sekantendreiecke an den Graphen gelegt und man erkennt, dass die größte Steigung ungefähr in der Mitte ist. Legt man statt der Sekanten Tangenten an den Graphen, so erhält man das gleiche Ergebnis.
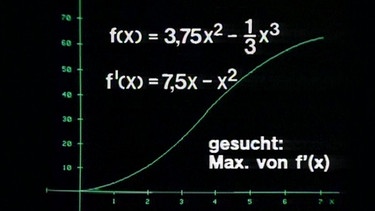
Die Steigung jeder Tangente entspricht dem Wert der 1. Ableitung in ihrem Berührpunkt, also der Funktionsgleichung der 1. Ableitung. Ihre Gleichung beträgt f’(x0) = 7,5x - x2 .
Um Extrempunkte dieser Ableitungsfunktion zu finden, bilden wir die Ableitung, also die 2. Ableitung f’’(x) = 7,5 – 2x .
Ihre Nullstelle liegt bei x = 3,75. Da die 3. Ableitung f’’’(x) = - 2 konstant negativ ist, bedeutet das, dass es sich um ein Maximum der 1. Ableitung, also ein Maximum der Steigung handelt.
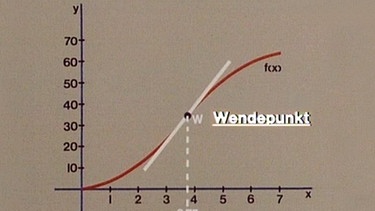
Dieser Punkt W der größten Steigung heißt Wendepunkt, weil nach einer ständigen Zunahme ab hier die Steigung wieder abnimmt.