Stetigkeit und Differenzierbarkeit Stetige Funktionen - Besonderheiten
Wir beantworten jetzt die Frage: Wann ist eine Funktion f(x) stetig? An verschiedenen Beispielen zeigen wir die Besonderheiten stetiger Funktionen auf.
Wann haben wir keine stetige Funktion? Einfach gesagt dann, wenn man den Verlauf des dazugehörigen Graphen nicht ohne Absetzen des Schreibstiftes zeichnen kann.
Die Zinsentwicklung beschreibt keine stetige Funktion: Ihre grafische Darstellung ist nicht ohne Absetzen des Schreibstiftes möglich. Eine stetige Funktion muss in einem gegebenen Intervall als glatte Kurve erscheinen, die an keiner Stelle unterbrochen ist. Für die Funktion bedeutet das, dass sie in jedem Punkt des Intervalls auch definiert sein muss.
Merkhilfe
Wann ist eine Funktion f(x) stetig?
Eine Funktion f(x), die in der Umgebung von x0 definiert ist, heißt an einer Stelle x0 des Definitionsbereichs stetig, wenn sie einen eindeutigen Grenzwert für x gegen x0 besitzt und wenn Grenzwert und Funktionswert an dieser Stelle gleich groß sind.
- Kurz mathematisch dargestellt: Der Limes von f(x) für x gegen x0 der Funktion ist gleich dem Funktionswert an der Stelle x0.
- Noch einfacher: Eine Funktion f(x) heißt in einem Intervall stetig, wenn f(x) an jeder Stelle des Intervalls stetig ist.
Aussagen über die Stetigkeit können nur für Stellen x0 aus dem Definitionsbereich gemacht werden. Denn an einer Definitionslücke gibt es die Funktion nicht und demnach kann auch keine Aussage über eine mögliche Stetigkeit getroffen werden. Bei Randpunkten an Intervallgrenzen kann aufgrund der nur einseitig möglichen Annäherung auch nur eine einseitige Stetigkeit nachgewiesen werden.
Weitere Besonderheiten für stetige Funktionen: Beispiel 1
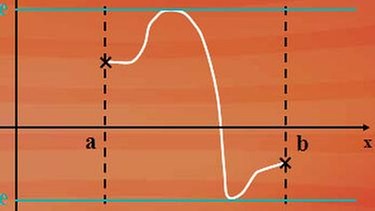
Nimmt eine in einem abgeschlossenen Intervall stetige Funktion f(x) in zwei Punkten des Intervalls Funktionswerte mit unterschiedlichen Vorzeichen an, so existiert zwischen den Punkten mindestens ein Punkt x0, für den die Funktion f(x0) gleich null ist.
Diese Erkenntnis fand Bernard Bolzano am Anfang des 19. Jahrhunderts. Der studierte Philosoph, Mathematiker und Physiker konstruierte als Erster eine Funktion, die überall stetig, aber an keiner Stelle differenzierbar ist.
Weitere Besonderheiten für stetige Funktionen: Beispiel 2
Obere und untere Grenze einer stetigen Funktion - klicken Sie bitte auf die Lupe.
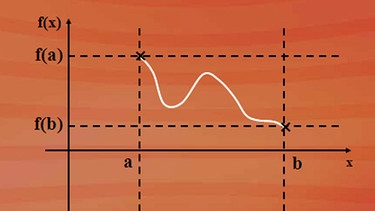
Noch ein weiteres Kriterium stetiger Funktionen: Eine in einem Intervall stetige Funktion nimmt in diesem Intervall ihre obere und ihre untere Grenze an.
Der deutsche Mathematiker Karl Wilhelm Weierstraß hat Ende des 19. Jahrhunderts die heute gültigen Bedingungen für stetige Funktionen zusammengefasst. Nach ihm ist eine Funktion f(x) in einem Punkt x0 dann stetig, wenn der Funktionswert der Annäherung gleich dem Funktionswert von x0 ist.
Weitere Besonderheiten für stetige Funktionen: Beispiel 3
Stetige Funktion ohne Nullstelle im gegebenen Intervall
Noch ein drittes Beispiel: Eine stetige Funktion, die im gegebenen Intervall keine Nullstelle hat, besitzt überall dasselbe Vorzeichen.