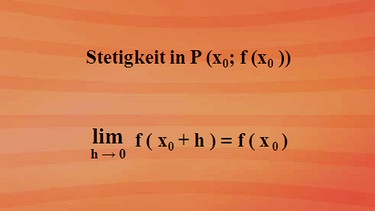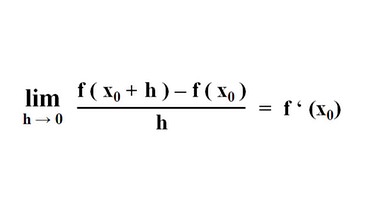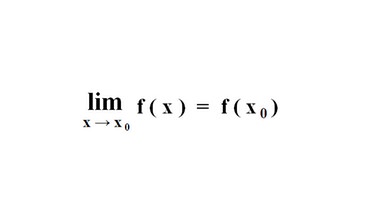Stetigkeit und Differenzierbarkeit Beispiele zur Differenzierbarkeit
Wir betrachten jetzt noch einige Beispiele für nicht stetige Funktionen, sozusagen Graphen von Funktionen mit Sprungstellen. Man unterscheidet dabei endliche und unendliche Sprungstellen.
Beispiele für endliche und unendliche Sprungstellen
Beispiele für endliche und unendliche Sprungstellen - klicken Sie bitte auf die Lupe.
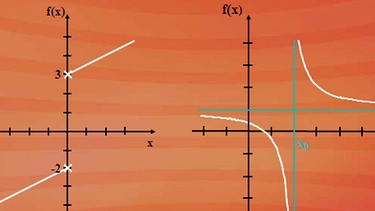
Zuerst ein Beispiel für eine endliche Sprungstelle: Der Graph von links kommend endet bei einem festen f(x)-Wert minus 2, beginnt wieder bei einem festen f(x)-Wert 3 – siehe nebenstehende Grafik. Ein Beispiel für eine unendliche Sprungstelle ergibt sich bei Hyperbeln. Der Graph von links kommend geht gegen minus unendlich. Er startet nach rechts weiterlaufend bei plus unendlich – klicken Sie bitte auf nebenstehende Abbildung.
Beispiel für unendliche Sprungstellen - klicken Sie bitte auf die Lupe.
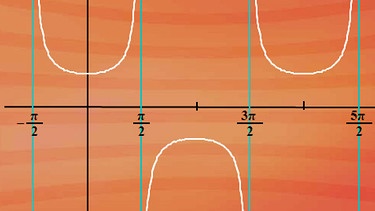
Unendliche Sprungstellen treten auch bei der Funktion f(x) = 1 durch cos x auf. Die Sprungstellen treten hier sogar periodisch auf – wie nebenstehende Abbildung zeigt.
Zusammenfassung
Stetige Funktionen
- Konstante Funktionen und lineare Funktionen sind im ganzen Definitionsbereich stetig.
- Dies gilt auch für jede ganz-rationale Funktion.
- Auch Exponentialfunktionen mit positiver Basis und die trigonometrischen Funktionen Sinus x und Kosinus x sind überall stetig.
Von der Stetigkeit zur Differenzierbarkeit
Wir wollen nun von der Stetigkeit auf die Differenzierbarkeit schließen. Wie Sie schon wissen, ist die Stetigkeit eine notwendige Bedingung der Differenzierbarkeit.
Für die Stetigkeit einer Funktion f(x) an einer Stelle x0 und einer Umgebung x0 plus h gilt nebenstehende Formulierung. Die Funktion f(x), die an der Stelle x = x0 und einer Umgebung von x0 definiert ist, heißt an der Stelle x0 stetig, wenn der Grenzwert von f(x0) plus h für h gegen null existiert und mit dem Funktionswert an der Stelle x0 übereinstimmt.
Von der Herleitung der Ableitungsregel wissen Sie noch, dass die Ableitung für die Steigung eines jeden Punktes der Funktion steht.
Berechnung der Steigung zwischen zwei Punkten - klicken Sie bitte auf die Lupe.
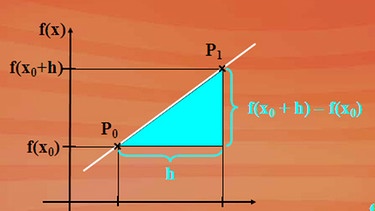
Die Steigung zwischen zwei Punkten P0 und P1 berechnet sich aus dem Quotienten der Differenz der Funktionswerte und der Differenz der x-Werte. Klicken Sie bitte auf nebenstehende Abbildung: Es ergibt sich für die Punkte P0 mit den Koordinaten x0 und f(x0) sowie P1 mit x0 plus h, und f(x0) plus h der Steigungsfaktor m mit f(x0) plus h minus f(x0) im Zähler durch x0 plus h minus x0 im Nenner.
Bedingung für Differenzierbarkeit
Sie wissen bereits, dass für den Fall h = 0 die Steigung einer Sekante in eine Tangentensteigung übergeht. Diese Tangentensteigung ist gleich der Ableitung der Funktion. Wenn dieser Grenzwert existiert, ist die Funktion differenzierbar. Siehe nebenstehende Abbildung.
Bedingung für Stetigkeit
Eine Funktion ist an einer Stelle x0 stetig, wenn sie dort definiert ist, der Grenzwert an dieser Stelle existiert und dieser gleich dem Funktionswert f an der Stelle x0 ist. Siehe nebenstehende Abbildung.
Fazit
Die Stetigkeit einer Funktion ist also eine notwendige Bedingung für die Differenzierbarkeit der Funktion. Das sagt auch aus, dass eine Funktion, die an einer Stelle x0 nicht stetig ist, dann an dieser Stelle auch nicht differenzierbar ist. Aber sie kann stetig sein und trotzdem nicht differenzierbar. Mehr dazu im folgenden Kapitel.