Einführung in die Integralrechnung Beispiel aus der Physik
Die erste Folge der Reihe "Integralrechnung" nähert sich dem Begriff des Integrals durch eine Strategie zur Berechnung der Fläche zwischen der Abszisse eines kartesischen Koordinatensystems und einem Abschnitt eines Graphen einer linearen oder nichtlinearen Funktion.
Wie groß ist die Fläche unter dem Graphen?
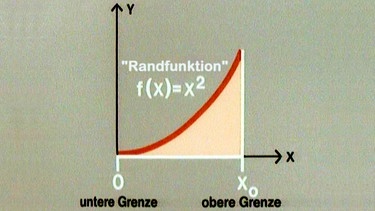
Zunächst wird die Fläche betrachtet, die von der Strecke der Abszisse zwischen den Werten 0 und x0, dem Graphen einer quadratischen Funktion zwischen den Werten 0 und x0 (der sog. Randfunktion) sowie dem Abschnitt einer Parallele zur y-Achse zwischen x0 und dem Graphen begrenzt wird.
Ein Gewichtsstück wird über einen Seilzug angehoben
Bevor dieses Problem gelöst wird, zeigt zunächst ein Beispiel aus der Physik die Bedeutung solch einer Flächenberechnung. Die Versuchsanordnung zeigt einen Seilzug, mit dem ein Gewichtsstück angehoben werden kann.
Das Potentiometer liefert eine dem Weg des Gewichtsstücks proportionale Spannung
Der Weg, den das Gewichtsstück zurücklegt, wird von einer Seilrolle auf ein Potentiometer übertragen, von dem eine dem Weg proportionale Spannung abgegriffen wird.
Am Dehnungsmessstreifen wird eine der Kraft im Seilzug proportionale Spannung abgegriffen
Zwischen den Seilzug und das Gewichtsstück ist ein Dehnungsmessstreifen eingefügt, das ist ein elektrisches Bauelement, das seinen Widerstand bei Krafteinwirkung ändert. An ihm wird eine der Kraft proportionale Spannung abgegriffen.
Der Stift des Messschreibers wird durch die beiden zugeführten Spannungen in x- bzw. y-Richtung ausgelenkt
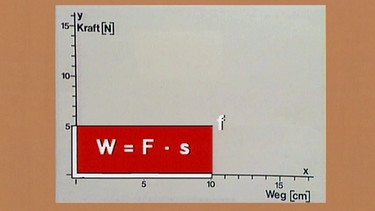
Diese beiden Spannungen werden einem Messschreiber zugeführt, der den Schreibstift analog zum Weg in horizontaler und analog zur Kraft in vertikaler Richtung auslenkt. Wird das Gewichtsstück mit m = 500 g um 10 cm nach oben bewegt, so schreibt der Stift eine horizontale Linie in Höhe von 5 N, also der Gewichtskraft auf das Gewichtsstück.
Das heißt, die Kraft ist während der Bewegung konstant geblieben.
Die Fläche des Rechtecks ist ein Maß für die aufgewendete Arbeit am Gewichtsstück
Kraft und Weg bilden die Seiten eines Rechtecks, dessen Fläche gleich dem Produkt aus Kraft und Weg ist. Also ist die Fläche ein Maß für die verrichtete Arbeit W an dem Gewichtsstück, W = F · s .