Einführung in die Integralrechnung Abgewandelter Versuch
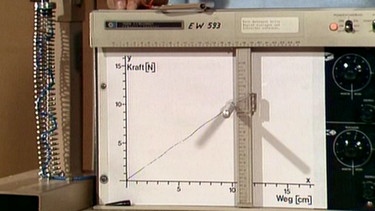
Bei einem abgewandelten Versuch wird nun das Gewichtsstück durch eine Schraubenfeder ersetzt.
Das Gewichtsstück ist durch eine Schraubenfeder ersetzt.
Die Zugkraft F der Schraubenfeder ist bei einer Dehnung s = 0 ebenfalls Null und nimmt proportional zur Dehnung zu.
Die Federkraft nimmt proportional zur Dehnung zu.
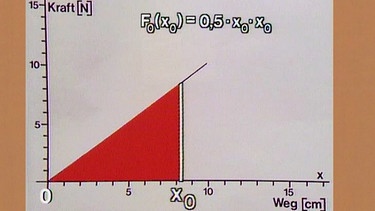
Erwartungsgemäß zeichnet der Messschreiber diesmal einen Abschnitt einer Ursprungsgeraden mit dem Anfangspunkt 0 und dem Endpunkt (10 cm/10 N).
Wie groß ist die Dreiecksfläche unter dem Graphen?
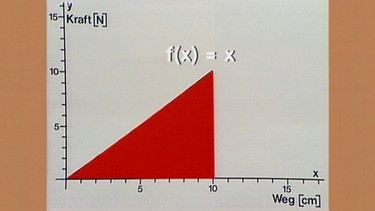
Die Fläche unter dem Graphen, also die Fläche eines rechtwinkeligen Dreiecks, ließe sich nun einfach nach der bekannten Formel Fläche ist gleich 0,5 mal Grundlinie mal Höhe, in diesem Fall A = 0,5 ·s ·F bzw. für die Arbeit W = 0,5 · s · F berechnen, die Sendung beschreitet aber einen anderen, universellen Lösungsweg, der nicht nur für den Spezialfall einer linearen Funktion geeignet ist.
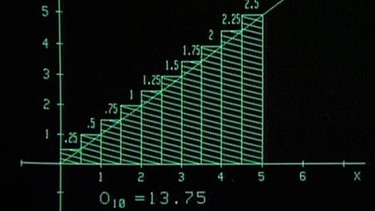
Die Dreiecksfläche wird näherungsweise als Summe der Flächen von 10 überstehenden Rechtecken (sog. Obersumme) betrachtet.
Die Dreiecksfläche wird näherungsweise als Summe der Flächen von 10 Rechtecken betrachtet, die allerdings nur an der rechten Seite dem Abstand der x-Achse zum Graphen entsprechen, an der linken oberen Ecke aber darüber hinaus ragen. Um die Rechen- und Zeichenarbeit zu beschleunigen, lässt man beides von einem PC erledigen. Die Summe der Rechtecksflächen beträgt demnach 13,75 . Dieser Näherungswert ist wegen der überstehenden Dreiecke etwas größer als der wahre Wert.
Nun wird einer anderer Weg der Annäherung gesucht:
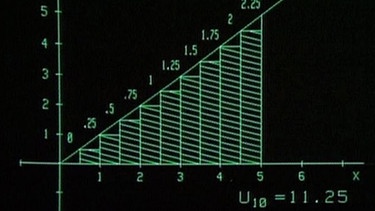
Die Dreiecksfläche wird näherungsweise als Summe der Flächen von 10 Rechtecken (sog. Untersumme) betrachtet, die den Graphen von unten berühren.
Der Rechner berechnet die Summe der Flächen von Rechtecken, die den Graphen von unten berühren. Die Summe der Rechtecksflächen beträgt diesmal 11,25, das ist ein etwas kleinerer Wert als der wahre Wert. Es handelt sich dabei um die sog. Untersumme, der größere Wert, s.o., heißt Obersumme.
Die Ober- bzw. Untersumme bei Unterteilung in 20 Rechtecke
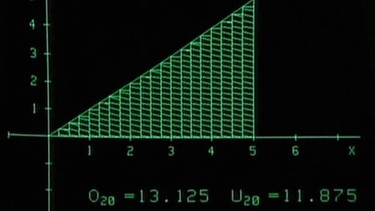
Die Methode lässt sich verfeinern, in dem man mehr schmälere Rechtecke berechnet und ihre Flächen addiert, jetzt z.B. zwanzig. Die Untersumme beträgt nun 11,875, die Obersumme 13,125.
Bei 100 kleinen und 100 großen Rechecken erhält man die Untersumme 12,375 und die Obersumme 12,625
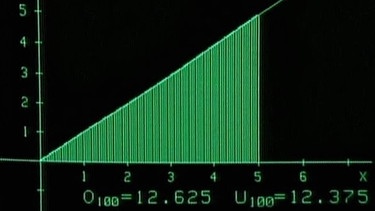
Bei 100 kleinen und 100 großen Rechecken erhält man die Untersumme 12,375 und die Obersumme 12,625. Die Werte der Untersumme und der Obersumme nähern sich also bei immer feinerer Unterteilung dem wahren Wert der Dreiecksfläche an.
Für beliebig viele Rechtecke erhält man schließlich den Grenzwert 12,50
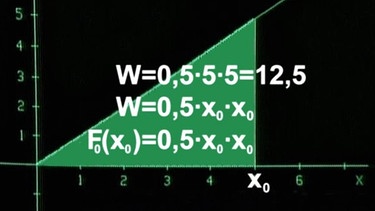
Für beliebig viele Rechtecke erhält man schließlich den Grenzwert 12,50. Er entspricht dem Wert der Dreiecksfläche bzw. hier der Arbeit, also W = 0,5 · 5 · 5 = 12,5 [J]. Bezeichnet man die untere Begrenzung des Dreiecks allgemein mit x0, so erhält man für die Arbeit
W = 0,5·x0·x0.
Für die Dreiecksfläche gilt oben stehende Formel. Klicken Sie bitte auf die Lupe.
Betrachtet man stattdessen allgemein die Dreiecksfläche, so ergibt sich für die Fläche F0(x0) = 0,5·x0·x0 . Die Schreibweise F0(x0) bedeutet "Fläche von 0 bis zum Wert x0", die Fläche ändert sich also mit dem Wert von x0 .