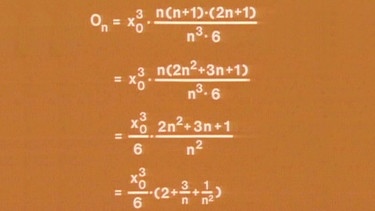Einführung in die Integralrechnung Flächenberechnung - Parabelbogen
Die Strategie "Rechtecksbildung – Summieren – Verfeinern", die bisher nur auf lineare Funktionen angewendet wurde, soll nun auf die Aufgabe vom Anfang, die Berechnung der Fläche zwischen einer waagrechten, einer senkrechten Strecke und einem Parabelbogen angewendet werden.

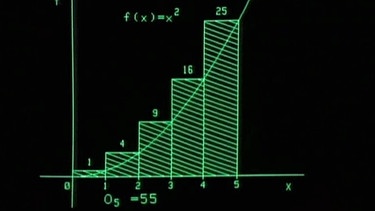
Dazu wird das gleiche Verfahren angewendet, wie bei der Bestimmung der Dreiecksfläche: Die eingeschlossene Fläche wird zunächst in fünf Rechtecke zerlegt, die über den Graphen hinausragen, ihre Obersumme O5 beträgt 55.
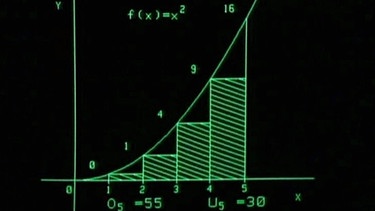
Die entsprechende Untersumme U5 der fünf den Graphen berührenden Rechtecke beträgt dagegen 30.
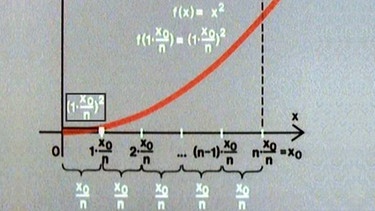
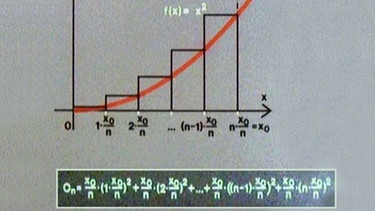
Dieses Verfahren wird nun nicht mit dem PC, sondern als Berechnung für einen allgemeinen Wert x0 der Funktion f(x) = x2 fortgesetzt. Teilt man die Stecke von 0 bis x0 auf der x-Achse in n Abschnitte, so hat jeder Abschnitt die Breite x0/n. Das erste Rechteck reicht dann von 0 bis 1· x0/n, das zweite von 1· x0/n bis 2·x0/n usw. und das n-te Rechteck bis n·x0/n, d.h. bis x0. Die Höhe des ersten Rechtecks errechnet sich zu (1·x0/n)2.
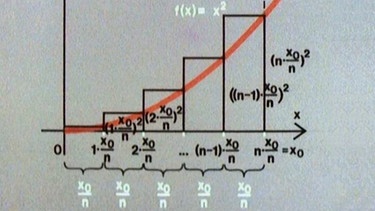
Das zweite Rechteck hat dann die Höhe (2·x0/n)2, das (n-1)te Rechteck die Höhe ((n-1)·x0/n)2 und das n-te Rechteck die Höhe (n·x0/n)2.
Die Obersumme On ergibt sich aus der Summe der n Rechtecke zu
On = (x0/n)(1·x0/n)2 + (x0/n)(2·x0/n)2 + ... + (x0/n)((n-1)·x0/n)2 + (x0/n)(n·x0/n)2.
Bei der Berechnung dieser Summe lässt sich zunächst x03/n3 ausklammern und wir erhalten:
On = (x03/n3)(12 + 22 + ... + (n-1)2 + n2).
Nach der Regel der vollständigen Induktion lässt sich der Ausdruck (12 + 22 + ... + (n-1)2 + n2) durch n(n+1)(2n+1)/6 ersetzen und wir erhalten
On = (x03/n3)(n(n+1)(2n+1)/6 .
Wenn der Bruch mit 1/n3 multipliziert wird, erhalten wir
On = x03·(n(n+1)(2n+1)/6n3.
Um die Rechtecke immer mehr zu verfeinern, muss n gegen Unendlich gehen, dazu formen wir die Gleichung in mehreren Schritte um und erhalten schließlich
On = (x03/6)(2+3/n+1/n2).
Für n => ∞ gilt 3/n => 0 und 1/n2 => 0 und wir erhalten letztlich On = x03/3 .
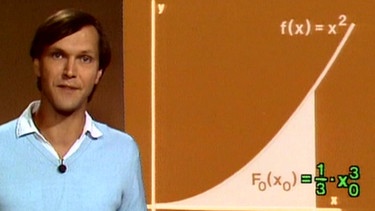
Führt man die gleiche Berechnung für die Untersumme Un durch, so erhält man auch hier den Grenzwert x03/3, Un also = x03/3 für n => ∞. Für einen beliebigen Wert x0 erhalten wird also F0(x0) = x03/3 und damit lässt sich die Fläche zwischen dem Parabelbogen, der x-Achse und der Parallele zur y-Achse durch x0 berechnen.
Testen Sie Ihr Wissen!