Telekolleg - Integralrechnung Fallversuch
Der Zusammenhang zwischen Beschleunigung, Zeit und Weg lässt sich auch in einem einfachen Fallversuch ermitteln.
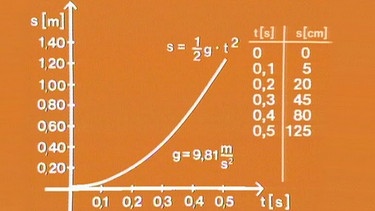
Ein Ball fällt mit der Erdbeschleunigung g ≈ 10 m/s2, seine Bewegung wird dabei zusammen mit einem Längenmaßstab mit einer Zeitlupenkamera aufgenommen. Die Ergebnisse des Messversuchs werden dann in einer Tabelle zusammengefasst.
Trägt man die Messwerte in ein Koordinatensystem ein, so lässt sich erkennen, dass der Graph der Zeit-Weg- Funktion eine Parabel darstellt, die Funktionsgleichung lautet s = 0,5·g·t2 mit g ≈ 10 m/s2 (der genaue Wert ist nur 2% kleiner, nämlich g = 9,81 m/s2).
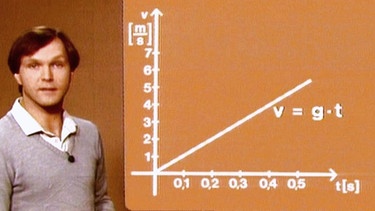
Die Geschwindigkeit dagegen ist der Zeit direkt proportional, der Graph der Zeit- Geschwindigkeit-Funktion ist eine Gerade mit der Steigung g und der Funktionsgleichung v = g · t .
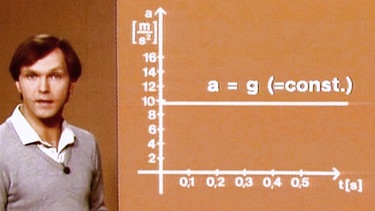
Die Beschleunigung g schließlich ist nahe der Erdoberfläche konstant, nämlich g = 9,81 m/s2 . Der Graph im Zeit-Beschleunigung- Diagramm ist daher eine Gerade parallel zur x-Achse bzw. t-Achse (Zeitachse).
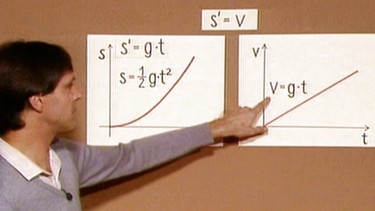
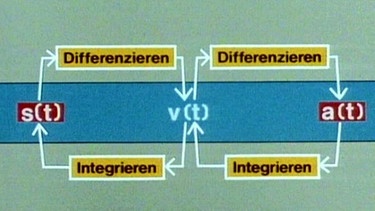
Bildet man die 1. Ableitung der Funktion s = 0,5·g·t2, so erhält man die Ableitungsfunktion s’ = 2·0,5·g·t = g·t. Der Vergleich mit der aus der Physik bekannten Formel v = g·t zeigt, das v die 1. Ableitung der Funktion s = f(t) ist, also gilt s’= v, die Geschwindigkeit ist die 1. Ableitung der Zeitfunktion des Weges.
Analog dazu ergibt die 1. Ableitung der Geschwindigkeit die Beschleunigung, v’ = a bzw. in diesem Spezialfall v’ = g.
Durch zweimaliges Differenzieren der Funktion s = f(t) gelangt man also zur Funktion a = f(t). Der Hauptsatz der Differential- und Integralrechnung besagt nun, dass auch die umgekehrte Operation möglich ist, d.h. durch zweimaliges Integrieren der Funktion a = f(t) erhält man die Funktion s = f(t).
Beispiel: Flugzeug
In einem Flugzeug kann durch das ständige Messen der Beschleunigungen die exakte Position durch Integrieren berechnet werden.
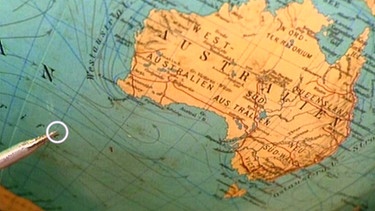
In einem Flugzeug zum Beispiel, das ja keinen klassischen Kilometerzähler besitzt, kann durch das ständige Messen der Beschleunigung in allen Richtungen die exakte Position durch Integrieren berechnet werden, hier beispielsweise 48°50’2“ südlicher Breite und 110°58’2“ östlicher Länge (E englisch für East).
Diese Angabe entspricht einer Position über dem Indischen Ozean südwestlich von Australien.
Wie das Modell zeigt, enthält das Positionsmessgerät drei Pendel für alle drei Raumachsen, da ja auch das Flugzeug in allen drei Achsrichtungen beschleunigt werden kann.
Die Abbildung zeigt das Gerät, in dem die drei winzigen Pendel mit den zugehörigen Winkelsensoren eingebaut sind. Damit die Pendel im Raum ihre Lage behalten, wird das System in seiner Lage mit einem rotierenden Kreisel stabilisiert. Das Gerät enthält zudem die elektronischen Rechenschaltungen zur Integration der Pendelausschläge und Berechnung der zurückgelegten Wegstrecken und letztlich auch zur Ansteuerung des Displays.