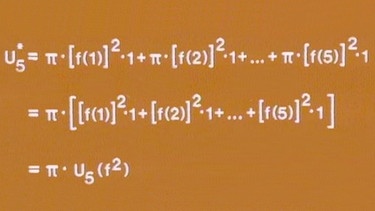Telekolleg - Integralrechnung Volumen von Rotationskörpern
Zur Berechnung des Volumens von Rotationskörpern greifen wir auf die bereits bekannte Methode der Flächenberechnung zurück. Mittels Unterteilung, Zylinderbildung und Verfeinerung erhalten wir das Volumen.
In der Geometrie, genauer im Bereich Stereometrie, kennt man den Begriff des Rotationskörpers. Ein solcher Rotationskörper entsteht, wenn man einen Abschnitt eines Funktionsgraphen um eine Achse rotieren lässt.
Verschiedene Rotationskörper
Lässt man den Draht mit der Form einer Randfunktion rotieren, so entsteht das Bild eines Rotationskörpers.
In der Sendung wurde zum Beispiel ein Draht in der Form des Graphen einer Wurzelfunktion in das Futter einer Bohrmaschine eingespannt. Der rotierende Draht wurde dann stroboskopisch beleuchtet und es ließ sich ein kelchförmiges Gebilde erkennen.
Auf gleiche Weise wird aus einem halbkreisförmigen Drahtstück als Rotationskörper eine Kugel.
Ein gerades Drahtstück, das etwa den Graph einer linearen Funktion darstellen könnte, ergibt als Rotationskörper einen Kegel.
Berechnung des Volumens
Bei der Berechnung des Volumens eines Rotationskörpers greift man auf die Methode der Flächenberechnung zurück.
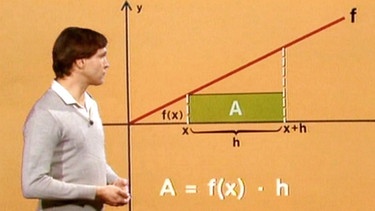
Bei der Berechnung des Volumens eines solchen Rotationskörpers greift man zunächst auf die bereits bekannte Methode der Flächenberechnung zurück. Die Fläche unter einer linearen Randfunktion f z.B. wird in eine Vielzahl von Rechtecken zerlegt. Die Fläche A eines solchen Rechtecks mit der Breite f(x) und der Höhe h hat die Größe A = f(x)·h .
Lässt man nun den Graphen der Funktion f um die x-Achse rotieren, so entsteht aus dem Rechteck mit der Fläche A ein Zylinder mit dem Volumen V.
Lässt man den Graphen der Funktion f um die x-Achse rotieren, so entsteht aus dem Rechteck mit der Fläche A ein Zylinder mit dem Volumen V.
Wie aus der Geometrie bekannt, ist das Volumen V eines Zylinders Grundfläche mal Höhe, wobei die Grundfläche eine Kreisfläche der Größe r2·π ist. Das Volumen des Rotationszylinder hat somit die Größe
V = π[f(x)]2·h.
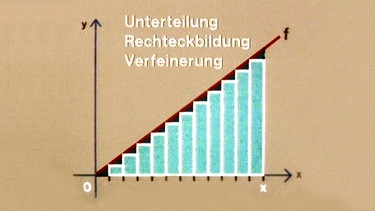
Bei der Methode zur Flächenberechnung wendet man die Schritte Unterteilung, Rechteckbildung und Verfeinerung an.
Bei der Methode zur Flächenberechnung wendet man die Schritte Unterteilung, Rechteckbildung und Verfeinerung an, bis ein Grenzwert für die Höhe der Rechtecke (Δh → 0) erreicht ist.
Unterteilung, Zylinderbildung und Verfeinerung
Bei der Volumenberechnung ist das Vorgehen entsprechend angepasst: Unterteilung, Zylinderbildung und Verfeinerung.
Analog zur Flächenberechnung lässt sich auch für die Zylinder im Kegel eine Ober- und Untersumme bilden. Für 5 Zylinder z.B. ist die Untersumme U5*= π[f(1)]2·1+ π[f(2)]2·1+ π[f(3)]2·1+ π[f(4)]2·1 + π[f(5)]2·1.
Nach dem Ausklammern von π und Zusammenfassen erhält man U5* = π· U5·(f2).
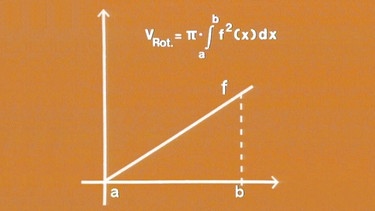
Führt man diese Rechnung weiter, so erhält man analog zur Flächenberechnung für die Volumenberechnung eines Rotationskörpers mit der Randfunktion f(x) und den Grenzen a und b für das Rotationsvolumen die Formel
Vrot. = π·a∫bf2(x) dx.
Testen Sie Ihr Wissen!