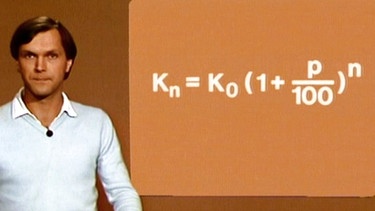Telekolleg - Integralrechnung Die Exponentialfunktion
Wir lernen die Zinseszinsformel kennen und erläutern sie anhand von grafischen Darstellungen. Die Formel lässt sich in eine Wachstumsfunktion umformen, die man auch für Beispiele aus der Biologie anwenden kann.
Wie viel Kapital sich nach n Jahren angesammelt hat, lässt sich mit der sog. Zinseszinsformel berechnen.
Das Wachstum einer Exponentialfunktion macht sich jeder Sparer zunutze, der sein Geld mit einem festen Zinssatz auf einem Konto angelegt hat und die anfallenden Zinsen ungeschmälert auf dem Konto belässt. Diese Zinsen werden dann im Folgejahr mitverzinst usw. Wie hoch sich das Kapital Kn nach n Jahren bei einem Grundkapital K0 und einem Zinssatz p (in Prozent) beläuft, lässt sich mit der sog. Zinseszinsformel berechnen: Kn = K0(1 + p/100)n .
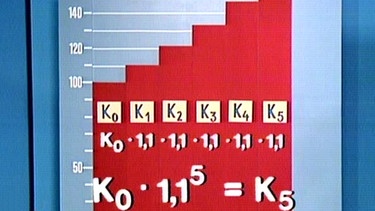
Diese Formel lässt sich anhand der Grafik leicht nachvollziehen, als Beispiel dient ein Zinssatz von 10% also p = 10, die Summe in der Klammer ist dann 1,1. Das Kapital nach einem Jahr ist K0·1,1, nach dem 2. Jahr (K0·1,1)1,1, nach dem 3. Jahr ((K0·1,1)1,1)1,1, nach dem 4. Jahr (((K0·1,1)1,1)1,1)1,1 und nach dem 5. Jahr ((((K0·1,1)1,1)1,1)1,1)1,1 bzw. in Potenzschreibweise K5 = K0·1,15.
Nach dem n-ten Jahr ist das Kapital dann auf Kn = K0·1,1n angewachsen.
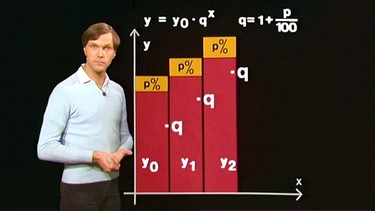
Statt des speziellen Zinssatzes p = 10% kann auch ein beliebiger Zinssatz p eingesetzt werden, statt 1,1 steht dann in der Formel (1 + p/100). Wenn man statt (1 + p/100) die Größe q einsetzt, lautet die Formel - wie oben angegeben - Kn = K0(1 + p/100)n bzw. Kn = K0·qn .
Diese Formel kann nun ganz allgemein für eine Wachstumsfunktion umgeformt werden: Man ersetzt K0 durch einen Startwert y0 und n durch x und erhält die Wachstumsformel y = y0 ·qx.
Beispiele aus der Biologie
Als erstes Beispiel wird das Wachstum einer Mäusekolonie von 60 Mäusen berechnet, die sich in jedem Monat um 50% vermehrt. Die Formel lautet für dieses Beispiel y = 60·1,5x
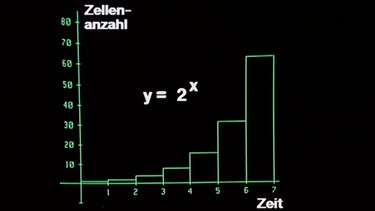
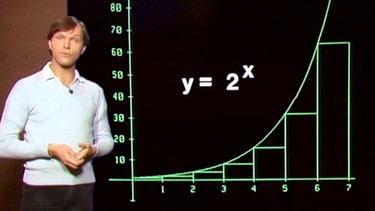
Ein weiteres Beispiel aus der Biologie ist das Zellwachstum. Eine Zelle teilt sich nach einer bestimmten Zeit Δt, nach der gleichen Zeit Δt teilen sich die zwei Zellen wieder usw. D.h. nach jedem Zeitabschnitt Δt verdoppelt sich die Zahl der Zellen (genügend Nahrungsangebot vorausgesetzt). Der Prozentsatz ist hier also 100% bzw. der Faktor q = 1 + 100/100 = 2. Die Wachstumsfunktion lautet daher y = 2x .
Trägt man die Zahl der Zellen nach jeweils einem Zeitabschnitt Δt in ein Säulendiagramm ein, so lässt sich das rasche Wachstum gut erkennen.
Betrachtet man dagegen eine sehr große Zellkolonie, z. B. die Hefezellen in einem Hefeteig, so lässt sich sie Vermehrung nicht mehr in diskreten Schritten beobachten, sie erscheint kontinuierlich.
Der Graph der Funktion ist dann nicht mehr treppenförmig, sondern verläuft stetig nach oben, ebenfalls mit der Funktionsgleichung y = 2x .