Telekolleg - Integralrechnung Die Logarithmusfunktion
Die Logarithmusfunktion ist die Umkehrung der Exponentialfunktion. Wie ist das zu verstehen?

Betrachten wir dazu zunächst die bekannte Zinseszinsformel K0(1 + p/100)x = Kx . Diese Exponentialfunktion besagt, dass nach einer Anzahl von x Jahren das Endkapital Kx erreicht wird.
Dreht man die Fragestellung um und will wissen, nach welcher Zahl von Jahren ein bestimmtes Endkapital erreicht wird, so handelt es sich um eine Umkehrung der Exponentialfunktion.
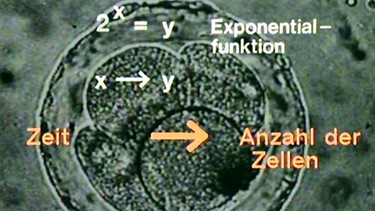
Beim Zellwachstum verdoppelt sich in einem Zeitabschnitt Δt die Zahl der Zellen, das Zellwachstum folgt der Exponentialfunktion 2x = y.
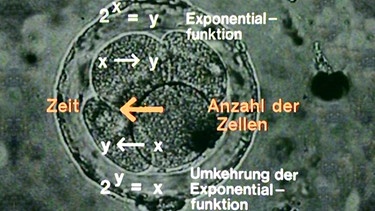
Dreht man auch hier die Fragestellung um und will wissen, nach welcher Zeit t eine bestimmt Zahl von Zellen entstanden ist, so lautet die Funktionsvorschrift 2y = x, es handelt sich auch hier um die Umkehrung der Exponentialfunktion.
Die Funktion 2y = x bedeutet, dass eine Zahl y gesucht wird, mit der 2 potenziert den Wert x ergibt. Nach y aufgelöst ergibt sich die Funktion y = log2 x, log2 x ist der Logarithmus zur Basis 2 von x.
Der Graph der Funktion y = log2 x lässt sich - wie die Graphik zeigt - punktweise mit Hilfe einer Wertetabelle zeichnen. Da die Logarithmusfunktion y = log2 x die Umkehrfunktion der Exponentialfunktion y = 2x ist, spiegeln sich die Graphen an der Spiegelgeraden y = x (rote Linie), so dass der Graph der Logarithmusfunktion auch durch Spiegeln der Exponentialfunktion gezeichnet werden kann.
Der Natürliche Logarithmus
Logarithmusfunktionen sind auch für alle anderen Basen a > 0 möglich, eine besondere Rolle spielen in der Mathematik der Logarithmus zur Basis 10, log10 x, abgekürzt lg x, und der Logarithmus zur Basis e, loge x, der sog. Natürliche Logarithmus, abgekürzt ln x (logarithmus naturalis).
Umwandlung in e-Funktion
Die Beziehung eln a = a lässt sich nutzen, um beliebige Exponentialfunktionen y = ax in e-Funktionen umzuwandeln: y = ax = (eln a)x = eln a · x.
Als erstes Beispiel soll y = 2x in eine in e-Funktion umgewandelt werden:
y = 2x = eln a · x ≈ e0,69 · x.
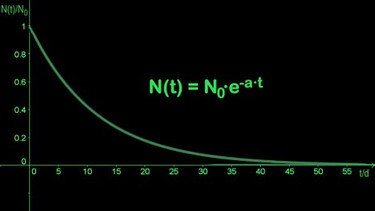
Das zweite Beispiel hat eine Basis a < 0: y = 0,5x = eln 0,5 · x ≈ e-0,69 · x .
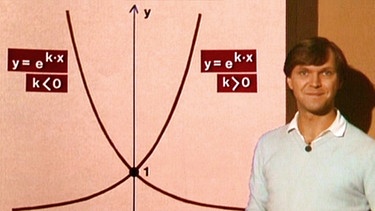
Der negative Exponent dieser e-Funktion weist darauf hin, dass der Graph - wie der von allen Exponentialfunktionen mit a < 1 - monoton fallend ist. Die Graphen von Exponentialfunktionen mit a > 1 dagegen sind monoton steigend.
Testen Sie Ihr Wissen!