Der Graph einer monoton fallenden Exponentialfunktion

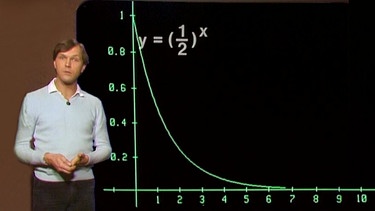
Bei den bisher betrachteten Exponentialfunktionen ist a > 1, daher steigt der Graph der Funktion stetig an. Betrachten wir nun als Beispiel den Graphen der Funktion y = 0,5^x, so zeigt sich, dass der Graph - beginnend bei y = 1 für y = 0,5⁰ - stetig fällt.

Man spricht in diesem Fall von exponentiellem Abnehmen.

Experiment zum exponentiellen Abnehmen

Versuchanordnung zur Absorption eines Lichtbündels in einer Flüssigkeit

Ein physikalisches Experiment zeigt dieses exponentielle Abnehmen: In einem Aquarium befindet sich eine gefärbte Flüssigkeit und ein Schwimmer, dessen Höhenlage über einen Seilzug auf eine Rolle übertragen wird. Die Rolle ist mit einem Potentiometer (Drehwiderstand mit Abgriff) verbunden, an dem eine der Höhenlage des Schwimmers bzw. der Höhe des Flüssigkeitsspiegels proportionale elektrische Spannung abgegriffen wird. Diese Spannung wird einem Messschreiber zugeführt, bei dem sie eine horizontale Auslenkung des Schreibstifts bewirkt. Unterhalb des Aquariums befindet sich eine Lampe, die ein Lichtbündel mit nahezu parallelen Randstrahlen senkrecht nach oben abstrahlt.

Das Lichtbündel wird auf der durchsichtigen Deckplatte des Aquariums von einer Fotozelle aufgefangen, die eine der Beleuchtungsstärke proportionale elektrische Spannung erzeugt. Diese wird ebenfalls dem Messschreiber zugeführt und hat dort eine vertikale Auslenkung des Schreibstifts zur Folge. Das Lichtbündel wird in der Flüssigkeit teils absorbiert, teils gestreut, so dass es - je nach Höhe des Flüssigkeitsspiegels - mehr oder weniger abgeschwächt wird.

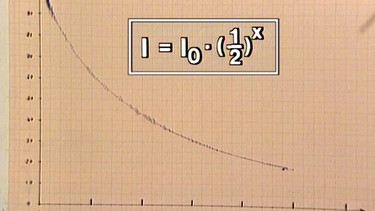
Bei einer bestimmten Höhe des Flüssigkeitsspiegels x₀ wird die Hälfte der Energie des Lichtbündels absorbiert, bei der doppelten Höhe 2x₀ nochmals die Hälfte, so dass die Beleuchtungsstärke nur noch ein Viertel beträgt usw. Lässt man nun die Flüssigkeit ablaufen, so sinkt der Flüssigkeitsspiegel bzw. die Schichtdicke der Flüssigkeit nimmt ab. Entsprechend wird das Lichtbündel weniger geschwächt, die Beleuchtungsstärke an der Fotozelle steigt und entsprechend auch die abgegebene Spannung.

Die Intensität des Lichtbündels nimmt exponentiell mit der Stärke der Flüssigkeitsschicht ab.

Der Messschreiber zeichnet eine beim Flüssigkeitsspiegel Null bis zur relativen Beleuchtungsstärke von 100% ansteigende Kurve bzw. - von Null ausgehend - für zunehmende Werte x des Flüssigkeitsspiegels eine abfallende Kurve. Die Beleuchtungsstärke I(x) folgt der Funktion I(x) = I₀·0,5^x .

Auch hier liegt also eine Exponentialfunktion vor.

Grafische Darstellung

Die Graphen der drei verschiedenen Typen von Exponentialfunktionen

Die Grafik zeigt die Graphen der drei verschiedenen Typen von Exponentialfunktionen: Ist der Exponent x der Funktion y = a^x gleich 1, also y = a¹, so gilt y = a, der Graph ist eine Parallele zur x-Achse. Für x > 1 sind alle Graphen monoton steigend, für x < 1 sind alle Graphen monoton fallend. Alle Graphen schneiden die y-Achse in dem gemeinsamen Punkt 0/1, denn bei x = 0 gilt y = a⁰ = 1. Alle Graphen verlaufen oberhalb der x-Achse und nähern sich ihr, ohne sie zu erreichen, die x-Achse ist ihre Asymptote.

Die Eulersche Zahl

Die Eulersche Zahl spielt in der Mathematik eine herausragende Rolle.

Die Eulersche Zahl e ≈ 2,7182818 spielt in der Mathematik eine herausragende Rolle. Sie lässt sich aus der schon bekannten Zinseszinsberechnung ableiten.

Kapitalzuwachs bei p = 100% und jährlicher Verzinsung

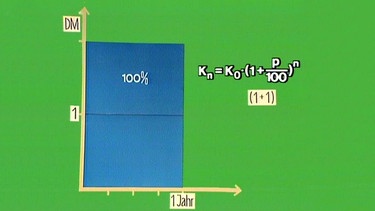
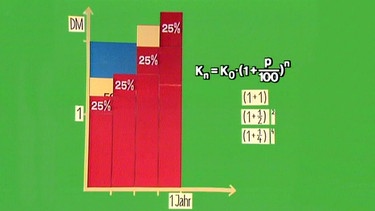
Wir betrachten das Wachstum eines Kapitals von 1 DM bei einer Verzinsung von p = 100%. Der Betrag in der Klammer der Zinseszinsformel K_n = K₀(1 + p/100)ⁿ ist dann (1 + 1).

Kapitalzuwachs bei p = 100% und halbjährlicher Verzinsung

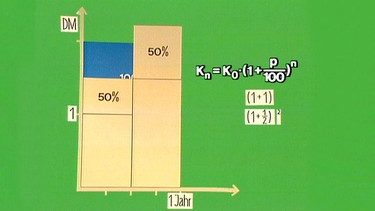
Wenn das Kapital nicht einmal jährlich verzinst wird, sondern zweimal, so kommen nach 0,5 Jahren 50% hinzu, nach einem Jahr zu diesen 150% dann 50% von 1,5 DM, insgesamt sind es dann 2,25 DM. Die Formel lautet nun K_n = K₀(1 + 0,5)².

Kapitalzuwachs bei p = 100% und vierteljährlicher Verzinsung

Verzinst man das Kapital vierteljährlich, so lautet die Formel K_n = K₀(1 + 0,25)⁴, das Kapital ist nach einem Jahr auf 2,44 DM gewachsen.

Für beliebig kurze Verzinsungszeitabschnitte strebt Kapitalzuwachs einem Grenzwert zu. Klicken Sie bitte auf die Lupe.

Wächst also bei immer kürzeren Verzinsungszeiträumen das Kapital in einem Jahr unbegrenzt? Dazu berechnen wir die Verzinsung für einen Verzinsungszeitraum von 0,125 Jahren, bei einem monatlichen Rhythmus, einem täglichen Rhythmus (1/360 Jahr), einem 1/10000 Jahr und schließlich 1/1000000 Jahr. Es zeigt sich, dass die in einem Jahr erzielte Summe nicht beliebig steigt, sondern einem Grenzwert zustrebt, für 1/1000000 Jahr ist er schon auf 8 Stellen genau und beträgt 2,7182818.

Leonhard Euler (1707 - 1783) entdeckte und berechnete die Zahl e

Für beliebig große Werte von n in der Formel a_n = (1 + 1/n)ⁿ erreicht a_n den Grenzwert e, für n → ∞ gilt dann e = lim_{n → ∞} (1 + 1/n)ⁿ Diese Zahl e ist benannt nach dem Basler Mathematiker Leonhard Euler, der sie entdeckte und berechnete.