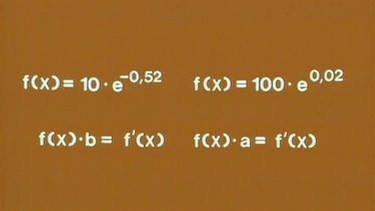Telekolleg - Integralrechnung Monoton abnehmende Exponentialfunktionen
Wir wenden uns jetzt monoton abnehmenden Exponentialfunktionen zu, also Funktionen mit negativer Wachstumsgeschwindigkeit. Beim radioaktiven Zerfall z.B. nimmt die Zahl der Atome eines bestimmten radioaktiven Isotops ständig ab.
Beispiel: radioaktiver Zerfall
Die Bahnen der alpha-Teilchen werden als Nebelspuren sichtbar.
Der Blick in eine sogenannte Nebelkammer zeigt, dass die von einem (gelb markierten) radioaktiven Präparat ausgesandten α-Teilchen (zweifach positiv geladene Kerne des Edelgases Helium) die Gasatome in der Nebelkammer ionisieren, das heißt elektrisch aufladen.
Um diese Ionen sammeln sich winzige Tröpfchen, die insgesamt als Nebelspuren sichtbar werden.
Die Aktivität des Isotops nimmt proportional zu der Exponentialfunktion ab.
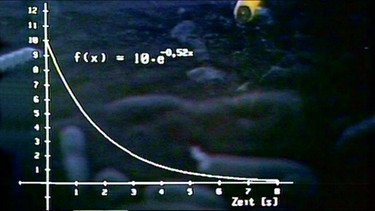
Misst man die Aktivität des Isotops – hier Polonium-211 - mit einem quantitativen Messgerät, z. B. einem Zählrohr, so lässt sich erkennen, dass diese rasch abnimmt. Die Auswertung ergibt eine monoton fallende Exponentialfunktion f(x) = 10·e-0,52·x. Dabei ist 0,52 die sog. Zerfallskonstante des Isotops.
Durch Auswertung der Exponentialfunktion lassen sich die Abnahmewerte bestimmen.
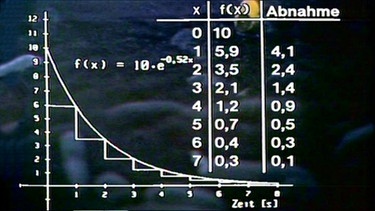
Mit Hilfe der Funktionsgleichung lassen sich die Werte von f(x) für x = 1 .... x = 7 berechnen und somit die zugehörigen Abnahmewerte bestimmen. Im Diagramm sind diese Werte wieder als Höhen der Sekantendreiecke eingezeichnet.
Die Abnahmewerte sind den zugehörigen Funktionswerten proportional.
In der Tabelle sind die berechneten Funktionswerte und die jeweils für Δx = 1 s ermittelten Abnahmewerte eingetragen. Man kann daraus ersehen, dass mit der abnehmenden Zahl von radioaktiven Atomen auch immer weniger von ihnen je Zeiteinheit zerfallen.
Bei der Auswertung der Tabelle lässt sich - analog zur monoton wachsenden Exponentialfunktion - erkennen, dass die Abnahmewerte proportional zu den Funktionswerten sind, der Proportionalitätsfaktor beträgt hier 0,7. Auch hier könnte man das Zeitintervall Δx beliebig verkleinern und erhielte schließlich statt der Sekantensteigungen Tangentensteigungen, also jeweils die Ableitung f’(x).
Ergebnisvergleich der beiden Experimente
Die Exponentialfunktionen sind ihren Ableitungen proportional.
In der Grafik sind die Ergebnisse der beiden Experimente - Bakterienwachstum und radioaktiver Zerfall - zusammengestellt. Demnach ist die Ableitung sowohl der monoton steigenden wie der monoton fallenden Exponentialfunktion proportional zu der zugehörigen Exponentialfunktion.
Die Normalparabel ist ihrer Ableitung nicht proportional.
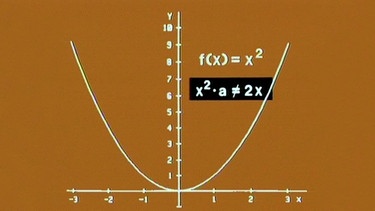
Haben diese Eigenschaft nur Exponentialfunktionen? Um diese Frage zu beantworten, bedarf es eines umfangreichen Beweises. Ein Beispiel legt aber nahe, dass bei anderen stetig steigenden und/oder fallenden Funktionen Funktion und Ableitung nicht gleich und auch nicht proportional sind. So hat die proportionale Funktion g(x) der Normalparabel f(x) = x2 die Gleichung g(x) = a· x2, die Ableitung lautet aber f ’(x) = 2x .