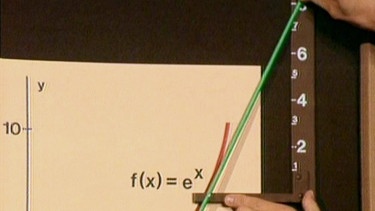Berechnung von 4 Funktionswerten der normalen e-Funktion

Um eine Regel für das Differenzieren von Exponentialfunktionen zu finden, muss die Größe des Proportionalitätsfaktors a in der Gleichung f(x)·a = f’(x) gefunden werden. Dazu wird in der Sendung eine experimentellgrafische Methode gewählt. Untersucht wird die Exponentialfunktion f(x) = e^x, dabei werden zunächst die Funktionswerte für x = 0, x = 1, x = 1,5 und x = 2 berechnet und in eine Tabelle eingetragen. Gerundet erhalten wir e⁰ = 1, e¹ = 2,7, e^1,5 = 4,5 und e² = 7,4 .

Grafische Ermittlung der Tangentensteigungen

Mit Hilfe eines sogenannten Tangentensteigungsmessgeräts wird dann die Tangentensteigung in den Punkten 0/1, 1/2,7, 1,5/4,5 und 2/7,4 ermittelt.

Funktionswerte und die zugehörigen Werte der Ableitung einer e-Funktion sind gleich.

Die grafisch gemessenen Steigungswerte werden in die Tabelle eingetragen und es zeigt sich, dass - im Rahmen der Messgenauigkeit - der Wert der Tangentensteigung und der zugehörige Funktionswert gleich sind.

Die e-Funktion ist ihrer Ableitung gleich.

Eingehende mathematische Untersuchungen zeigen, dass dieses Ergebnis für alle e-Funktionen zutrifft: Die Funktion y = e^x ist gleich ihrer Ableitung y’ = e^x, y = e^x = y’.

Enthält der Exponent der e-Funktion einen Faktor, z.B. f(x) = e^2x, so werden die bekannten Regeln des Differenzierens sinngemäß angewendet:

Ableitung einer e-Funktion mit einem Faktor im Exponenten

Die e-Funktion selbst bleibt unverändert, der Faktor im Exponenten bildet in der Ableitung nun aber ein Produkt mit der ursprünglichen e-Funktion, d.h. hier: f’(x) = 2·e^2x.