Sie wissen nun, dass man in Dreiecken Seiten und Winkel berechnen kann, wenn bestimmte Teilstücke gegeben sind. Zur Berechnung hatten wir einfache Hilfsmittel gefunden: im rechtwinkligen Dreieck waren das der Satz von Pythagoras, der Höhensatz und die Kathetensätze sowie die Winkelfunktionen Sinus, Kosinus und Tangens. Auch für beliebige Dreiecke hatten wir ein Werkzeug gefunden: den Sinussatz. Aber dieser Sinussatz ist nur beschränkt einsetzbar. Es ist eben ein Spezialwerkzeug, das im allgemeinen Dreieck nur dann verwendet werden kann, wenn drei Teilstücke des Dreiecks gegeben sind, von denen mindestens eines ein Winkel ist, der zu einer gegebenen Seite gegenüberliegt. Was ist aber, wenn das nicht der Fall ist?
Dann müssen wir ein neues Werkzeug finden, das die Bearbeitung dieses neuen Spezialfalles ermöglicht.

Bisher war es nicht möglich, Seiten und Winkel in einem Dreieck zu berechnen, wenn zwei Seiten mit dem von ihnen eingeschlossenen Winkel gegeben sind. Der Sinussatz funktioniert hier nicht.

Ein Beispiel

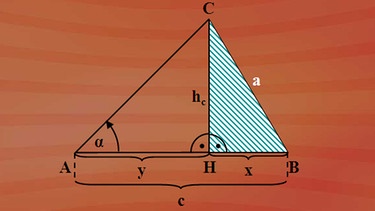
Gegeben ist das beliebige Dreieck ABC, bei dem die Seitenlängen b und c sowie der von diesen beiden Seiten eingeschlossene Winkel alpha bekannt sind - siehe die Abbildung oben. Zur Anwendung des Sinussatzes fehlt die dem Winkel gegenüberliegende Seitenlänge a.

Vielleicht kann man in dem Dreieck ABC Teildreiecke finden, in denen Altbekanntes angewendet werden kann? Nach dieser Methode haben wir doch auch den Sinussatz gefunden. Da haben wir es mit rechtwinkligen Teildreiecken geschafft.

Rechtwinklige Teildreiecke

Aufteilung in zwei rechtwinklige Dreiecke: Bitte klicken Sie auf die Lupe.

Die Höhe auf c teilt das Dreieck ABC in die beiden rechtwinkligen Dreiecke AHC und HBC. Betrachten wir mal das Teildreieck HBC, in dem die uns nicht bekannte Seitenlänge a vorkommt. Es ist ein rechtwinkliges Dreieck mit der Hypotenuse a und den Katheten h_c und HB. Dieses HB ist eine Teilstrecke der Seite c, bezeichnen wir sie mal mit x. Und weil wir schon bei der Vergabe von Symbolen sind, bezeichnen wir die verbleibende Streckenlänge der Seite c mit y.

Erstes Grundwerkzeug: Satz von Pythagoras

Satz von Pythagoras: Bitte klicken Sie auf die Lupe.

Als Grundwerkzeug steht uns der Satz von Pythagoras zur Verfügung: Im Dreieck HBC gilt Hypotenuse, hier a zum Quadrat ist gleich Kathete x zum Quadrat plus Kathete h_c zum Quadrat. Wir wollen eine Beziehung zwischen Seiten und Winkeln, da neben den Seitenlängen b und c der Winkel alpha gegeben ist. Dazu betrachten wir das rechtwinklige Teildreieck AHC.

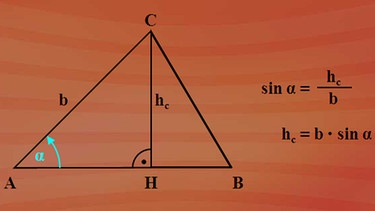
Teildreieck AHC

Vom Winkel alpha aus gesehen  ist die Seite h_c Gegenkathete und b die Hypotenuse. Sinus alpha ist gleich Gegenkathete h_c durch Hypotenuse b. Und da wir h_c nicht kennen, formen wir die Gleichung nach h_c um und erhalten h_c ist b mal Sinus alpha. 

Unser Ziel ist, einen Zusammenhang zwischen den drei Dreiecksseiten und dem Winkel alpha zu finden, denn dann wäre die fehlende Seitenlänge zu berechnen. Fassen wir zusammen, was wir bisher erkannt haben.