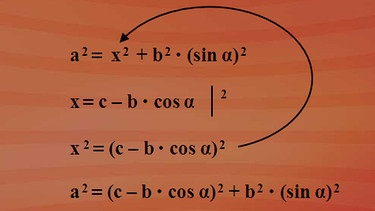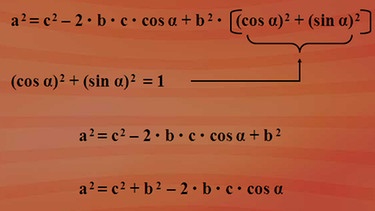"a hoch zwei ist gleich x hoch zwei plus h_c hoch zwei". h_c ist uns nicht bekannt, jedoch kennen wir bereits eine Gleichung mit h_c : "h_c ist b mal Sinus alpha". Somit ist "h_c hoch zwei gleich b hoch zwei mal Sinus alpha hoch zwei". Das passt genau in die Ausgangsgleichung "a Quadrat gleich x Quadrat plus h_c Quadrat". Wir erhalten "a Quadrat ist x Quadrat plus b Quadrat mal Sinus alpha zum Quadrat".

Weitere Berechnung: Bitte klicken Sie auf die Lupe.

Nun müssen wir nur noch die Länge x über Seitenlängen und Winkel des Dreiecks ABC ausdrücken. Die Seitenlänge x bildet mit der Seitenlänge y die Seitenlänge c des Dreiecks ABC. Etwas umgeformt erhalten wir für x: x ist gleich c minus y. Und y ist im rechtwinkligen Teildreieck AHC die Ankathete des Winkels alpha.

Anwendung des Kosinus

Anwendung des Kosinus - bitte klicken Sie auf die Lupe.

Kosinus alpha ist gleich Ankathete y durch Hypotenuse b. Nach y umgeformt: "y ist gleich b mal Kosinus alpha". Diesen Ausdruck setzen wir für y in unsere Gleichung "x ist c minus y" ein und erhalten "x gleich c minus b mal Kosinus alpha".

Zusammenfassung der Teilergebnisse

Jetzt haben wir eine Möglichkeit, aus b, c und alpha die Seitenlänge a des Dreiecks ABC zu berechnen. Fassen wir dazu unsere Teilergebnisse zusammen:

Wir hatten bereits die Gleichung "a Quadrat ist x Quadrat plus b Quadrat mal Sinus alpha zum Quadrat". Neu dazu kam: "x ist c minus b mal Kosinus alpha". Das "x Quadrat" in der ersten Gleichung stört. Quadrieren wir aber die zweite Gleichung, erhalten wir "x hoch zwei ist Klammer auf c minus b mal Kosinus alpha, Klammer zu zum Quadrat". Dieser Ausdruck lässt sich für x hoch zwei einsetzen. Es führt zur Gleichung "a Quadrat ist gleich c minus b mal Kosinus alpha in Klammern zum Quadrat plus b Quadrat mal Sinus alpha zum Quadrat".

Verschönern des Werkzeugs

Wir haben eine Gleichung, in der nur noch die Längen der Dreiecksseiten des Dreiecks ABC mit dem gegebenen Winkel alpha vorkommen. Jetzt wollen wir unsere gefundene Beziehung zwischen Seiten und Winkeln des Dreiecks ABC einer mathematischen Kosmetik unterziehen.

Mathematische "Kosmetik"

Summenschreibweise: Bitte klicken Sie auf die Lupe.

Als erstes bilden wir die Summenschreibweise des auftretenden zweiten Binoms. Den weiteren Rechenverlauf entnehmen Sie bitte nebenstehender Grafik - bitte klicken Sie auf die Lupe.

Zusammenhang zwischen Sinus und Kosinus: Bitte klicken Sie auf die Lupe.

Jetzt benötigen wir wieder etwas aus früheren Folgen: die Sinus- und Kosinusfunktion. Damals haben wir einen Zusammenhang zwischen Sinus und Kosinus gefunden: "Kosinus alpha zum Quadrat plus Sinus alpha zum Quadrat ist gleich eins". Dieses damalige Ergebnis kommt uns jetzt zugute.

Wir können "Kosinus alpha zum Quadrat plus Sinus alpha zum Quadrat" mit eins ersetzen. So erhalten wir eine vereinfachte Beziehung mit "a Quadrat ist c Quadrat minus zwei mal b mal c mal Kosinus alpha plus b Quadrat". Das stellen wir noch um, dann erhalten wir eine Gleichung, die man sich besser merken kann - für das Ergebnis klicken Sie bitte auf die Lupe in obenstehender Grafik.

Fazit: Kosinussatz im beliebigen Dreieck

Wir haben es also geschafft, eine Beziehung zwischen den Seiten und einem Winkel des Dreiecks herzustellen. Die Herleitung haben wir in einem spitzwinkligen Dreieck vorgenommen. Die gefundene Beziehung trägt den Namen "Kosinussatz im beliebigen Dreieck".