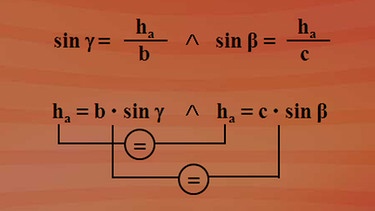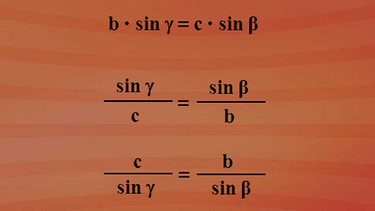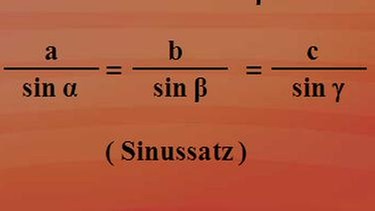Grundkurs Mathematik (14) 14.2. Die Herleitung des Sinussatzes
Jetzt teilen wir das Dreieck anders auf und können so neue Beziehungen herstellen: Das Ergebnis ist der Sinussatz.
Sinus Alpha durch a ist gleich Sinus Beta durch b. Oder als Kehrbruch: a zu Sinus Alpha ist gleich b zu Sinus Beta - das ist eine wunderschöne Beziehung. Aber was ist mit der Seite c oder dem Winkel Gamma?
Ein allgemeines Dreieck
Nehmen wir nicht die Höhe auf der Seite c, sondern die Höhe auf der Seite a zur Teilung des beliebigen Dreiecks in zwei rechtwinklige Teildreiecke. Dann sieht das Ganze wie in der nebenstehenden Grafik aus.
Die Teildreiecke heißen jetzt ABH und AHC. Beide sind rechtwinklig und haben somit Hypotenuse und Katheten. Im Teildreieck AHC gilt "Sinus von Gamma ist gleich Gegenkathete ha durch Hypotenuse b". Im Teildreieck ABH gilt: "Sinus Beta ist gleich Gegenkathete ha durch Hypotenuse c". Beide Gleichungen bilden wieder ein Gleichungssystem.
Das Gleichungssystem nach h auflösen
Eine Beziehung zwischen Seiten und Winkeln - klicken Sie bitte auf die Lupe.
Nach ha aufgelöst, ergeben sich die Gleichungen "ha ist gleich b mal Sinus Gamma" und "ha gleich c mal Sinus Beta". Die linken Seiten stimmen überein, somit müssen auch die rechten Seiten der beiden Gleichungen übereinstimmen und es ergibt sich: "b mal Sinus Gamma ist gleich c mal Sinus Beta" - eine Beziehung zwischen Seiten und Winkeln.
Der Zusammenhang
Wichtig ist, dass Sie die umgeformten Gleichungen "Sinus Gamma durch c ist gleich Sinus Beta durch b" oder als Kehrbruch "c durch Sinus Gamma ist b durch Sinus Beta" in Zusammenhang mit der ersten Beziehung "a durch Sinus Alpha ist gleich b durch Sinus Beta" sehen. Denn hier stimmen die beiden rechten Gleichungsseiten überein, demnach müssen auch die beiden linken übereinstimmen und man kann zusammenfassend sagen:
Zusammenfassung: Der Sinussatz
a zu Sinus Alpha verhält sich wie b zu Sinus Beta und das wiederum wie c zu Sinus Gamma. Diesen Zusammenhang bezeichnen wir als Sinussatz.