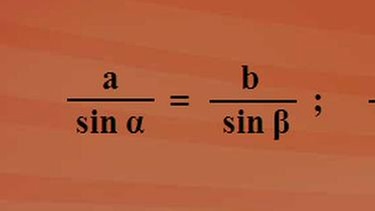Grundkurs Mathematik (14) 14.3. Der Sinussatz: Bedeutung und Gültigkeit
Wie lässt sich der Sinussatz allgemein formulieren? Und wo hat er überall Gültigkeit? Wie sieht es in stumpfwinkligen Dreiecken aus?
Man kann den Sinussatz, der einen Zusammenhang zwischen den Seiten und den Winkeln in einem beliebigen Dreieck herstellt, auch allgemein formulieren:
Allgemeine Formulierung: Der Sinussatz
Der Sinussatz - klicken Sie bitte auf die Lupe.
"In einem Dreieck sind für alle drei Seiten und alle drei Innenwinkel die Quotienten aus einer Seitenlänge und dem Sinus des gegenüberliegenden Winkels gleich groß."
Jeder der drei Quotienten des Sinussatzes stellt eine Beziehung zwischen einer Seite und dem gegenüberliegenden Winkel dar. Oder anders formuliert, in jedem ebenen Dreieck verhalten sich die Längen von zwei Seiten wie die Sinuswerte der gegenüberliegenden Winkel. Man kann es drehen und wenden, wie man möchte. Es muss auch nicht der Quotient aus Seite zum Sinuswert des gegenüberliegenden Winkels gewählt werden, es könnte auch der Quotient Sinus des Winkels zur Länge der gegenüberliegenden Seite genommen werden. Aufgegliedert sieht es dann folgendermaßen aus:
Die Bedeutung des Sinussatzes:
a zu Sinus Alpha ist gleich b zu Sinus Beta, b zu Sinus Beta ist c zu Sinus Gamma und a zu Sinus Alpha ist gleich c zu Sinus Gamma. Oder mit den Kehrwerten: Sinus Alpha zu a ist gleich Sinus Beta zu b und so weiter. Klicken Sie bitte auf neben stehendes Bild.
Die einzelnen Gleichungen zeigen, dass man mit Hilfe des Sinussatzes die restlichen Bestimmungsstücke eines beliebigen Dreiecks berechnen kann, wenn drei Stücke gegeben sind, von denen mindestens eines ein Winkel ist, der einer gegebenen Seite gegenüberliegt.
Der Sinussatz in stumpfwinkligen Dreiecken
Wie sieht es bei stumpfwinkligen Dreiecken aus, also bei Dreiecken, bei denen ein Winkel größer als 90 Grad ist? Unser gewonnener Sinussatz gilt auch für stumpfwinklige Dreiecke! Wer es nicht glauben möchte, der kann sich im Begleitbuch zur Sendung davon überzeugen. Hier wird auch gezeigt, dass nur für konstruierbare Dreiecke Lösungen erzielt werden können.